Dnevnik po bazi. Opredelitev logaritma in njegovih lastnosti: teorija in reševanje problemov

(iz grščine λόγος - "beseda", "relacija" in ἀριθμός - "število") številke b temelji na a(log α b) imenujemo takšno število c, In b= a c, to je zapisi log α b=c in b=ac so enakovredne. Logaritem je smiseln, če je a > 0, a ≠ 1, b > 0.

Z drugimi besedami logaritemštevilke b temelji na A formuliran kot eksponent, na katerega je treba povečati število a da dobim številko b(logaritem obstaja samo za pozitivna števila).

Iz te formulacije sledi, da je izračun x= log α b, je enakovredno reševanju enačbe a x =b.

Na primer:

log 2 8 = 3, ker je 8 = 2 3 .

Naj poudarimo, da navedena formulacija logaritma omogoča takojšnjo določitev vrednost logaritma, ko število pod znakom logaritma deluje kot določena potenca osnove. Dejansko formulacija logaritma omogoča utemeljitev, da če b=a c, nato logaritem števila b temelji na a enako z. Jasno je tudi, da je tema logaritmov tesno povezana s temo potence števila.

Izračunavanje logaritma se imenuje logaritem. Logaritem je matematična operacija logaritmiranja. Pri logaritmiranju se produkti faktorjev pretvorijo v vsote členov.

Potenciranje je matematična operacija inverzna logaritmu. Med potenciranjem se dana baza dvigne do stopnje izražanja, nad katero se izvaja potenciranje. V tem primeru se vsote členov pretvorijo v produkt faktorjev.

Pogosto se uporabljajo realni logaritmi z osnovami 2 (binarni), Eulerjevim številom e ≈ 2,718 (naravni logaritem) in 10 (decimalni).

Vklopljeno na tej stopnji je priporočljivo upoštevati vzorci logaritmov dnevnik 7 2 , ln √ 5, lg0,0001.

In vnosi lg(-3), log -3 3.2, log -1 -4.3 nimajo smisla, saj je v prvem od njih pod znakom logaritma postavljeno negativno število, v drugem - negativno število v osnovi, v tretji pa - tako negativno število pod znakom logaritma kot enoto v osnovi.

Pogoji za določitev logaritma.

Ločeno je vredno razmisliti o pogojih a > 0, a ≠ 1, b > 0, pod katerimi dobimo definicija logaritma. Poglejmo, zakaj so bile sprejete te omejitve. Pri tem nam bo pomagala enakost oblike x = log α b, ki se imenuje osnovna logaritemska identiteta, ki neposredno izhaja iz zgoraj navedene definicije logaritma.

Vzemimo pogoj a≠1. Ker je ena na poljubno potenco enako ena, potem velja enakost x=log α b lahko obstaja samo takrat, ko b=1, vendar bo log 1 1 poljubno realno število. Da bi odpravili to dvoumnost, vzamemo a≠1.

Dokažimo nujnost pogoja a>0. pri a=0 Glede na formulacijo logaritma lahko obstaja le, ko b=0. In temu primerno potem dnevnik 0 0 je lahko katero koli realno število, ki ni nič, saj je nič na katero koli potenco, ki ni nič, nič. To dvoumnost lahko odpravi pogoj a≠0. In kdaj a<0 morali bi zavrniti analizo racionalnih in iracionalnih vrednosti logaritma, saj je stopnja z racionalnim in iracionalnim eksponentom definirana samo za nenegativne baze. Zaradi tega je pogoj določen a>0.

In zadnji pogoj b>0 izhaja iz neenakosti a>0, ker je x=log α b, in vrednost stopnje s pozitivno osnovo a vedno pozitivno.

Značilnosti logaritmov.

Logaritmi zaznamuje izrazit Lastnosti, kar je pripeljalo do njihove široke uporabe za znatno olajšanje mukotrpnih izračunov. Ko se premaknemo »v svet logaritmov«, se množenje spremeni v veliko lažje seštevanje, deljenje v odštevanje, potenciranje in pridobivanje korena pa v množenje oziroma deljenje z eksponentom.

Formulacijo logaritmov in tabelo njihovih vrednosti (za trigonometrične funkcije) je leta 1614 prvič objavil škotski matematik John Napier. Logaritemske tabele, ki so jih povečali in podrobno opisali drugi znanstveniki, so se pogosto uporabljale v znanstvenih in inženirskih izračunih in so ostale pomembne vse do uporabe elektronskih kalkulatorjev in računalnikov.

Definicija logaritma

Logaritem b na osnovo a je eksponent, na katerega je treba dvigniti a, da dobimo b.

Številka e v matematiki je običajno označevanje meje, do katere stremi izraz

Številka e je iracionalno število- število, ki ni sorazmerno z ena, ga ni mogoče natančno izraziti ne kot celo število ne kot ulomek racionalnoštevilo.

Pismo e- prva črka latinske besede exponere- razkazovati se, od tod tudi ime v matematiki eksponentno- eksponentna funkcija.

številka eširoko uporablja v matematiki in v vseh vedah, ki tako ali drugače uporabljajo matematične izračune za svoje potrebe.

Logaritmi. Lastnosti logaritmov

Definicija: Logaritem pozitivnega števila b na njegovo osnovo je eksponent c, na katerega je treba dvigniti število a, da dobimo število b.

Osnovna logaritemska identiteta:

7) Formula za selitev na novo bazo:

lna = log e a, e ≈ 2,718…

Težave in testi na temo "Logaritmi. Lastnosti logaritmov"

• Logaritmi - Pomembne teme za pregled Enotnega državnega izpita iz matematike

Za uspešno opravljanje nalog na to temo morate poznati definicijo logaritma, lastnosti logaritmov, osnovno logaritemsko istovetnost, definicije decimalnega in naravnega logaritma. Glavne vrste problemov na to temo so problemi, ki vključujejo računanje in transformacijo logaritemskih izrazov. Oglejmo si njihovo rešitev na naslednjih primerih.

rešitev: Z uporabo lastnosti logaritmov dobimo

rešitev: Z uporabo lastnosti stopinj dobimo

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Lastnosti logaritmov, formulacije in dokazi.

Logaritmi imajo več značilne lastnosti. V tem članku si bomo ogledali glavne lastnosti logaritmov. Tu bomo podali njihove formulacije, zapisali lastnosti logaritmov v obliki formul, prikazali primere njihove uporabe in tudi dokazali lastnosti logaritmov.

Navigacija po straneh.

Osnovne lastnosti logaritmov, formule

Za lažjo zapomnitev in uporabo si predstavljajmo osnovne lastnosti logaritmov v obliki seznama formul. V naslednjem odstavku bomo podali njihove formulacije, dokaze, primere uporabe in potrebna pojasnila.

Lastnost logaritma enote: log a 1=0 za katero koli a>0, a≠1.

Logaritem števila, enaka osnovi: log a a=1 za a>0, a≠1.

Lastnost logaritma potence osnove: log a a p =p, kjer je a>0, a≠1 in p poljubno realno število.

Logaritem produkta dveh pozitivnih števil: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
in lastnost logaritma produkta n pozitivnih števil: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Lastnost logaritma količnika: , kjer je a>0, a≠1, x>0, y>0.

Logaritem potence števila: log a b p =p·log a |b| , kjer so a>0, a≠1, b in p takšna števila, da je stopnja b p smiselna in b p >0.

Posledica: , kjer je a>0, a≠1, n – naravno število, večji od ena, b>0.

Posledica 1: , a>0 , a≠1 , b>0 , b≠1 .

Posledica 2: , a>0 , a≠1 , b>0 , p in q so realna števila, q≠0 , zlasti za b=a imamo .

Formulacije in dokazi lastnosti

Nadaljujemo s formulacijo in dokazom pisnih lastnosti logaritmov. Vse lastnosti logaritmov so dokazane na podlagi definicije logaritma in osnovnega principa, ki iz nje sledi logaritemska identiteta, kot tudi lastnosti stopnje.

Začnimo z lastnosti logaritma ena. Njegova formulacija je naslednja: logaritem enote je enak nič, tj. log a 1=0 za katero koli a>0, a≠1. Dokaz ni težaven: ker je a 0 =1 za vsak a, ki izpolnjuje zgornje pogoje a>0 in a≠1, potem enakost log a 1=0, ki jo je treba dokazati, neposredno sledi iz definicije logaritma.

Navedimo primere uporabe obravnavane lastnosti: log 3 1=0, log1=0 in .

Pojdimo na naslednjo lastnost: logaritem števila, ki je enako osnovi, je enak ena, to je log a a=1 za a>0, a≠1. Dejansko, ker je a 1 =a za vsak a, potem je po definiciji logaritma log a a=1.

Primeri uporabe te lastnosti logaritmov so enakosti log 5 5=1, log 5,6 5,6 in lne=1.

Logaritem potence števila, ki je enak osnovi logaritma, je enak eksponentu. Ta lastnost logaritma ustreza formuli oblike log a a p =p, kjer je a>0, a≠1 in p – poljubno realno število. Ta lastnost izhaja neposredno iz definicije logaritma. Upoštevajte, da vam omogoča, da takoj navedete vrednost logaritma, če je mogoče število pod znakom logaritma predstaviti kot potenco osnove; o tem bomo več govorili v članku o izračunu logaritmov.

Na primer, log 2 2 7 =7, log10 -4 =-4 in .

Logaritem produkta dveh pozitivnih števil x in y enako zmnožku logaritmi teh števil: log a (x y)=log a x+log a y, a>0 , a≠1 . Dokažimo lastnost logaritma produkta. Zaradi lastnosti stopnje a log a x+log a y =a log a x ·a log a y in ker je po glavni logaritemski istovetnosti log a x =x in log a y =y, potem je log a x ·a log a y =x · y. Tako je log a x+log a y =x·y, iz česar po definiciji logaritma sledi enakost, ki jo dokazujemo.

Pokažimo primere uporabe lastnosti logaritma produkta: log 5 (2 3)=log 5 2+log 5 3 in .

Lastnost logaritma zmnožka lahko posplošimo na zmnožek končnega števila n pozitivnih števil x 1 , x 2 , …, x n kot log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. To enakost lahko brez težav dokažemo z metodo matematične indukcije.

Na primer, naravni logaritem produkta lahko nadomestimo z vsoto treh naravnih logaritmov števil 4, e in.

Logaritem količnika dveh pozitivnih števil x in y je enaka razliki med logaritma teh števil. Lastnost logaritma količnika ustreza formuli oblike , kjer so a>0, a≠1, x in y nekaj pozitivnih števil. Veljavnost te formule je dokazana kot tudi formula za logaritem produkta: saj , potem po definiciji logaritma .

Tukaj je primer uporabe te lastnosti logaritma: .

Pojdimo naprej lastnost logaritma potence. Logaritem stopnje je enak zmnožku eksponenta in logaritma modula osnove te stopnje. Zapišimo to lastnost logaritma potence kot formulo: log a b p =p·log a |b|, kjer so a>0, a≠1, b in p takšna števila, da je stopnja b p smiselna in b p >0.

Najprej dokažemo to lastnost za pozitivni b. Osnovna logaritemska istovetnost nam omogoča, da število b predstavimo kot log a b , potem je b p =(a log a b) p , dobljeni izraz pa je zaradi lastnosti potence enak a p·log a b . Tako pridemo do enakosti b p =a p·log a b, iz katere po definiciji logaritma sklepamo, da je log a b p =p·log a b.

To lastnost moramo še dokazati za negativni b. Pri tem upoštevamo, da je izraz log a b p za negativni b smiseln samo za sode eksponente p (ker mora biti vrednost stopnje b p večja od nič, sicer logaritem ne bo imel smisla), in v tem primeru b p =|b| str. Potem je b p =|b| p =(a log a |b|) p =a p·log a |b| , od koder je log a b p =p·log a |b| .

na primer in ln(-3) 4 =4·ln|-3|=4·ln3 .

Izhaja iz prejšnje lastnosti lastnost logaritma iz korena: logaritem n-tega korena je enak zmnožku ulomka 1/n z logaritmom radikalnega izraza, to je, kjer je a>0, a≠1, n naravno število, večje od ena, b>0 .

Dokaz temelji na enakosti (glej definicijo eksponenta z delnim eksponentom), ki velja za vsak pozitivni b, in lastnosti logaritma eksponenta: .

Tukaj je primer uporabe te lastnosti: .

Zdaj pa dokažimo formula za premik na novo logaritemsko osnovo prijazen . Za to je dovolj dokazati veljavnost enakosti log c b=log a b·log c a. Osnovna logaritemska identiteta nam omogoča, da število b predstavimo kot log a b , potem pa log c b=log c a log a b . Ostane še uporaba lastnosti logaritma stopnje: log c a log a b =log a b·log c a . S tem je dokazana enakost log c b=log a b·log c a, kar pomeni, da je dokazana tudi formula za prehod na novo osnovo logaritma .

Pokažimo nekaj primerov uporabe te lastnosti logaritmov: in .

Formula za prehod na novo bazo vam omogoča, da nadaljujete z delom z logaritmi, ki imajo "priročno" bazo. Uporabite ga lahko na primer za spreminjanje v naravne ali decimalne logaritme, tako da lahko izračunate vrednost logaritma iz tabele logaritmov. Formula za premik na novo bazo logaritma v nekaterih primerih omogoča tudi iskanje vrednosti danega logaritma, ko so znane vrednosti nekaterih logaritmov z drugimi bazami.

Pogosto uporabljen poseben primer formule za prehod na novo osnovo logaritma s c=b obrazca. To kaže, da sta log a b in log b a medsebojno inverzni števili. npr. .

Pogosto se uporablja tudi formula, ki je primerna za iskanje vrednosti logaritmov. Za potrditev naših besed bomo pokazali, kako se lahko uporabi za izračun vrednosti logaritma oblike . Imamo . Za dokazovanje formule je dovolj, da uporabimo formulo za premik na novo osnovo logaritma a: .

Ostaja še dokazati lastnosti primerjave logaritmov.

Uporabimo nasprotno metodo. Recimo, da za a 1 >1, a 2 >1 in a 1 2 ter za 0 1 velja log a 1 b≤log a 2 b. Na podlagi lastnosti logaritmov lahko te neenakosti prepišemo kot in in iz njih sledi, da je log b a 1 ≤log b a 2 oziroma log b a 1 ≥log b a 2. Nato po lastnostih potenc z iz istih razlogov izpolnjeni morata biti enakosti b log b a 1 ≥b log b a 2 in b log b a 1 ≥b log b a 2, to je a 1 ≥a 2 . Tako smo prišli do protislovja s pogojem a 1 2. S tem je dokaz zaključen.

Osnovne lastnosti logaritmov

• Materiali za lekcijo
• Prenesite vse formule

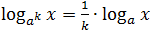
Logaritme, tako kot vsa števila, lahko seštevamo, odštevamo in preoblikujemo na vse načine. Ker pa logaritmi niso ravno navadna števila, so tukaj pravila, ki se imenujejo glavne lastnosti.

Ta pravila vsekakor morate poznati - brez njih ni mogoče rešiti niti enega resnega logaritemskega problema. Poleg tega jih je zelo malo - vsega se lahko naučiš v enem dnevu. Pa začnimo.

Seštevanje in odštevanje logaritmov

Razmislite o dveh logaritmih z enakimi osnovami: log a x in log a y. Nato jih je mogoče seštevati in odštevati in:

Torej je vsota logaritmov enaka logaritmu produkta, razlika pa je enaka logaritmu količnika. Opomba: ključni trenutek tukaj - enake podlage. Če so razlogi drugačni, ta pravila ne delujejo!

Te formule vam bodo pomagale izračunati logaritemski izraz, tudi če ne upoštevate njegovih posameznih delov (glejte lekcijo "Kaj je logaritem"). Oglejte si primere in si oglejte:

Naloga. Poiščite vrednost izraza: log 6 4 + log 6 9.

Ker imajo logaritmi enake osnove, uporabimo formulo za vsoto:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Naloga. Poišči vrednost izraza: log 2 48 − log 2 3.

Osnove so enake, uporabljamo formulo razlike:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Naloga. Poišči vrednost izraza: log 3 135 − log 3 5.

Osnove so spet enake, tako da imamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kot lahko vidite, so prvotni izrazi sestavljeni iz "slabih" logaritmov, ki se ne izračunajo posebej. Toda po preobrazbah se izkažejo precej normalne številke. Mnogi so zgrajeni na tem dejstvu testne pole. Da, na Enotnem državnem izpitu so izrazi, podobni testom, na voljo z vso resnostjo (včasih skoraj brez sprememb).

Ekstrakcija eksponenta iz logaritma

Zdaj pa malo zapletimo nalogo. Kaj pa, če je osnova ali argument logaritma potenca? Nato lahko eksponent te stopnje vzamemo iz znaka logaritma po naslednjih pravilih:

• log a x n = n · log a x ;
• 
• 

To je enostavno opaziti zadnje pravilo sledi prvima dvema. Vendar si ga je vseeno bolje zapomniti - v nekaterih primerih bo to znatno zmanjšalo količino izračunov.

Seveda so vsa ta pravila smiselna, če se upošteva ODZ logaritma: a > 0, a ≠ 1, x > 0. In še nekaj: naučite se uporabljati vse formule ne le od leve proti desni, ampak tudi obratno , tj. Številke pred znakom za logaritem lahko vnesete v sam logaritem. To je tisto, kar se najpogosteje zahteva.

Naloga. Poišči vrednost izraza: log 7 49 6 .

Znebimo se stopnje v argumentu s prvo formulo:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Naloga. Poiščite pomen izraza:

[Napis k sliki]

Upoštevajte, da imenovalec vsebuje logaritem, katerega osnova in argument sta natančni potenci: 16 = 2 4 ; 49 = 7 2. Imamo:

[Napis k sliki]

Mislim, da zadnji primer zahteva nekaj pojasnila. Kam so izginili logaritmi? Do zadnjega trenutka delamo samo z imenovalcem. Osnovo in argument logaritma, ki stoji tam, smo predstavili v obliki potenc in vzeli eksponente - dobili smo "trinadstropni" ulomek.

Zdaj pa poglejmo glavni del. Števec in imenovalec vsebujeta isto število: log 2 7. Ker je log 2 7 ≠ 0, lahko ulomek skrajšamo - 2/4 bo ostalo v imenovalcu. Po aritmetičnih pravilih lahko štiri prenesemo v števec, kar je bilo tudi storjeno. Rezultat je bil odgovor: 2.

Prehod na novo podlago

Ko sem govoril o pravilih za seštevanje in odštevanje logaritmov, sem posebej poudaril, da delujejo le z enakimi osnovami. Kaj pa, če so razlogi drugačni? Kaj pa, če nista natančni potenci istega števila?

Na pomoč pridejo formule za prehod na novo podlago. Oblikujmo jih v obliki izreka:

Naj bo podan logaritem log a x. Potem za vsako število c, tako da je c > 0 in c ≠ 1, velja enakost:

[Napis k sliki]

Zlasti, če nastavimo c = x, dobimo:

[Napis k sliki]

Iz druge formule sledi, da lahko osnovo in argument logaritma zamenjamo, vendar je v tem primeru celoten izraz "obrnjen", tj. logaritem se pojavi v imenovalcu.

Te formule redko najdemo v običajnih številskih izrazih. Kako priročni so, je mogoče oceniti le z odločitvijo logaritemske enačbe in neenakosti.

Vendar pa obstajajo težave, ki jih sploh ni mogoče rešiti, razen s prehodom na novo podlago. Oglejmo si nekaj teh:

Naloga. Poiščite vrednost izraza: log 5 16 log 2 25.

Upoštevajte, da argumenta obeh logaritmov vsebujejo natančne potence. Izločimo indikatorje: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Zdaj pa "obrnimo" drugi logaritem:

[Napis k sliki]

Ker se zmnožek pri preurejanju faktorjev ne spremeni, smo mirno pomnožili štiri in dva, nato pa se lotili logaritmov.

Naloga. Poiščite vrednost izraza: log 9 100 lg 3.

Osnova in argument prvega logaritma sta natančni potenci. Zapišimo to in se znebimo indikatorjev:

[Napis k sliki]

Zdaj pa se znebimo decimalnega logaritma s premikom na novo osnovo:

[Napis k sliki]

Osnovna logaritemska identiteta

Pogosto je treba v procesu reševanja število predstaviti kot logaritem na dano osnovo. V tem primeru nam bodo pomagale naslednje formule:

1. n = log a a n

2. V prvem primeru postane število n eksponent v argumentu. Število n je lahko karkoli, saj je le logaritemska vrednost.

   Druga formula je pravzaprav parafrazirana definicija. Temu se reče: osnovna logaritemska identiteta.

   Pravzaprav, kaj se zgodi, če število b dvignemo na takšno potenco, da število b na to potenco da število a? Tako je: rezultat je enako število a. Še enkrat natančno preberite ta odstavek - veliko ljudi se mu zatakne.

   Tako kot formule za prehod na novo bazo je osnovna logaritemska identiteta včasih edina možna rešitev.

   [Napis k sliki]

   Upoštevajte, da je log 25 64 = log 5 8 - preprosto smo vzeli kvadrat iz osnove in argumenta logaritma. Ob upoštevanju pravil za množenje potenc z isto bazo dobimo:

   [Napis k sliki]

   Če kdo ne ve, je bila to prava naloga iz enotnega državnega izpita :)

   Logaritemska enota in logaritemska ničla

   Za zaključek bom podal dve identiteti, ki ju težko imenujemo lastnosti - prej sta posledici definicije logaritma. Nenehno se pojavljajo v težavah in, presenetljivo, delajo težave tudi »naprednejšim« študentom.

   1. log a a = 1 je logaritemska enota. Zapomnite si enkrat za vselej: logaritem katere koli baze a te same baze je enak ena.
   2. log a 1 = 0 je logaritemska ničla. Osnova a je lahko karkoli, če pa argument vsebuje ena, je logaritem enak nič! Ker je 0 = 1 neposredna posledica definicije.

   To so vse lastnosti. Bodite prepričani, da jih vadite v praksi! Prenesite goljufijo na začetku lekcije, jo natisnite in rešite naloge.

   Logaritem. Lastnosti logaritma (seštevanje in odštevanje).

   Lastnosti logaritma izhajajo iz njegove definicije. In tako logaritem števila b temelji na A je definiran kot eksponent, na katerega je treba dvigniti število a da dobim številko b(logaritem obstaja samo za pozitivna števila).

   Iz te formulacije sledi, da je izračun x=log a b, je enako reševanju enačbe a x =b. na primer dnevnik 2 8 = 3 Ker 8 = 2 3 . Formulacija logaritma omogoča utemeljitev, da če b=a c, nato logaritem števila b temelji na a enako z. Jasno je tudi, da je tema logaritmov tesno povezana s temo potence.

   Z logaritmi, kot z drugimi številkami, lahko storite operacije seštevanja, odštevanja in preobraziti na vse možne načine. Ker pa logaritmi niso povsem običajna števila, veljajo tu svoja posebna pravila, ki se imenujejo glavne lastnosti.

   Seštevanje in odštevanje logaritmov.

   Vzemimo dva logaritma z enakimi osnovami: log a x in prijavite se. Nato je mogoče izvajati operacije seštevanja in odštevanja:

   Kot vidimo, vsota logaritmov je enako logaritmu produkta in Razlika logaritmi- logaritem količnika. Še več, to velja, če številke A, X in pri pozitivno in a ≠ 1.

   Pomembno je omeniti, da so glavni vidik v teh formulah iste baze. Če so razlogi drugačni, ta pravila ne veljajo!

   Pravila za seštevanje in odštevanje logaritmov z enakimi osnovami se berejo ne le od leve proti desni, ampak tudi obratno. Kot rezultat imamo izreka za logaritem produkta in logaritem količnika.

   Logaritem produkta dveh pozitivnih števil je enaka vsoti njunih logaritmov ; če preoblikujemo ta izrek, dobimo naslednje, če številke A, x in pri pozitivno in a ≠ 1, to:

   Logaritem količnika dveh pozitivnih števil je enaka razliki med logaritmama dividende in delitelja. Povedano drugače, če številke A, X in pri pozitivno in a ≠ 1, to:

   Za rešitev uporabimo zgornje izreke primeri:

   Če številke x in pri so torej negativni formula logaritma produkta postane brez pomena. Zato je prepovedano pisati:

   saj izraza log 2 (-8) in log 2 (-4) sploh nista definirana (logaritemska funkcija pri= dnevnik 2 X definiran samo za pozitivne vrednosti argumenta X).

   Izrek o produktu uporabna ne samo za dva, ampak tudi za neomejeno število dejavnikov. To pomeni, da za vsako naravno k in morebitna pozitivna števila x 1 , x 2 , . . . ,x n obstaja identiteta:

   Od izrek o logaritemskem kvocientu Dobimo lahko še eno lastnost logaritma. Splošno znano je, da log a 1 = 0, torej

   To pomeni, da obstaja enakost:

   Logaritma dveh vzajemnih števil iz istega razloga se bodo med seboj razlikovali samo po predznaku. Torej:

   Logaritem. Lastnosti logaritmov

   Logaritem. Lastnosti logaritmov

   Razmislimo o enakosti. Sporočite nam vrednosti in in želimo najti vrednost .

   To pomeni, da iščemo eksponent, s katerim ga moramo nagniti, da dobimo .

   Pustiti spremenljivka lahko prevzame poljubno realno vrednost, potem so za spremenljivke uvedene naslednje omejitve: o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″ />

   Če poznamo vrednosti in in se soočamo z nalogo iskanja neznanke, potem se v ta namen uvede matematična operacija, ki se imenuje logaritem.

   Da bi našli vrednost, ki jo vzamemo logaritem števila Avtor: osnova :

   Logaritem števila na njegovo osnovo je eksponent, na katerega ga je treba dvigniti, da dobimo .

   To je osnovna logaritemska identiteta:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   je v bistvu matematični zapis definicije logaritma.

   Matematična operacija logaritma je inverzna operaciji potenciranja, torej lastnosti logaritmov so tesno povezane z lastnostmi stopnje.

   Naštejmo glavne lastnosti logaritmov:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Naslednja skupina lastnosti vam omogoča, da eksponent izraza predstavite pod znakom logaritma ali stoji na dnu logaritma v obliki koeficienta pred znakom logaritma:

   6.

   7.

   8.

   9.

   Naslednja skupina formul omogoča prehod od logaritma z dano osnovo k logaritmu s poljubno osnovo in se imenuje formule za prehod na novo bazo:

   10.

   12. (posledica iz lastnosti 11)

   

   Naslednje tri lastnosti niso dobro znane, vendar se pogosto uporabljajo pri reševanju logaritemskih enačb ali pri poenostavljanju izrazov, ki vsebujejo logaritme:

   13.

   14.

   15.

   Posebni primeri:

   — decimalni logaritem

   — naravni logaritem

   Pri poenostavljanju izrazov, ki vsebujejo logaritme, se uporablja splošen pristop:

   1. Predstavljamo decimalke v obliki navadnih.

   2. Mešane številke predstavljeni kot nepravi ulomki.

   3. Števila na osnovi logaritma in pod znakom logaritma razstavimo na enostavne faktorje.

   4. Vse logaritme skušamo reducirati na isto osnovo.

   5. Uporabi lastnosti logaritmov.

   Oglejmo si primere poenostavitve izrazov, ki vsebujejo logaritme.

   Primer 1.

   Izračunajte:

   Poenostavimo vse eksponente: naša naloga je, da jih reduciramo na logaritme, katerih osnova je enako številu kot osnova eksponenta.

   ==(po lastnosti 7)=(po lastnosti 6) =

   Nadomestimo kazalnike, ki smo jih dobili v prvotni izraz. Dobimo:

   Odgovor: 5,25

   Primer 2. Izračunajte:

   

   Zmanjšajmo vse logaritme na osnovo 6 (v tem primeru se bodo logaritmi iz imenovalca ulomka "preselili" v števec):

   Razčlenimo števila pod logaritmom na preproste faktorje:

   Uporabimo lastnosti 4 in 6:

   Predstavimo zamenjavo

   Dobimo:

   Odgovor: 1

   Logaritem . Osnovna logaritemska identiteta.

   Lastnosti logaritmov. Decimalni logaritem. Naravni logaritem.

   Logaritem pozitivno število N na osnovo (b > 0, b 1) je eksponent x, na katerega je treba dvigniti b, da dobimo N .

   Ta vnos je enakovreden naslednjemu: b x = N .

   Primeri: dnevnik 3 81 = 4, ker je 3 4 = 81;

   dnevnik 1/3 27 = – 3, saj je (1/3) - 3 = 3 3 = 27.

   Zgornjo definicijo logaritma lahko zapišemo kot identiteto:

   

   Osnovne lastnosti logaritmov.

   2) log 1 = 0, saj b 0 = 1 .

   3) Logaritem produkta je enak vsoti logaritmov faktorjev:

   4) Logaritem količnika je enak razliki med logaritma dividende in delitelja:

   5) Logaritem potence je enak zmnožku eksponenta in logaritma njegove osnove:

   Posledica te lastnosti je naslednja: logaritem korena enako logaritmu radikalno število deljeno s potenco korena:

   

   6) Če je osnova logaritma stopinja, potem vrednost inverz eksponenta lahko vzamemo kot log rimo:

   

   Zadnji dve lastnosti lahko združimo v eno:

   

   7) Formula modula prehoda (tj. prehod iz ene baze logaritma v drugo):

   

   V posebnem primeru, ko N=a imamo:

   

   Decimalni logaritem klical osnovni logaritem 10. Označena je z lg, tj. dnevnik 10 n= dnevnik n. Logaritmi števil 10, 100, 1000, . p so 1, 2, 3, …, tj. imajo toliko pozitivnega

   enot, koliko ničel je v logaritemskem številu za ena. Logaritmi števil 0,1, 0,01, 0,001, . p so –1, –2, –3, …, tj. imajo toliko negativnih enic, kolikor je ničel v logaritemskem številu pred ena (vključno z nič celimi števili). Logaritmi drugih števil imajo ulomek, ki se imenuje mantisa. Celi del logaritma se imenuje značilnost. Za praktično uporabo so najbolj primerni decimalni logaritmi.

   Naravni logaritem klical osnovni logaritem e. Označujemo ga z ln, tj. dnevnik e n= dnevnik n. številka e je iracionalen, njegova približna vrednost je 2,718281828. Je meja, h kateri teži število (1 + 1 / n) n z neomejenim povečanjem n(cm. prvi čudovita meja na strani "Omejitve". številska zaporedja»).
   Čeprav se zdi čudno, so se naravni logaritmi izkazali za zelo priročne pri izvajanju različnih vrst operacij, povezanih z analizo funkcij. Računanje logaritmov na osnovo e izvede veliko hitreje kot zaradi katerega koli drugega razloga.

• Kaj je danes potrebno za posvojitev otroka v Rusiji? Posvojitev v Rusiji poleg odgovorne osebne odločitve vključuje številne postopke državnega preverjanja kandidatov. Težka izbira za pripravljalna faza prispeva k več […]
• Brezplačne informacije o TIN ali OGRN iz davčnega registra po vsej Rusiji - informacije o državni registraciji lahko dobite na portalu enotnih davčnih storitev pravne osebe, samostojni podjetniki, […]
• Kazen za vožnjo brez dokumentov (vozniško dovoljenje, zavarovanje, STS) Včasih zaradi pozabljivosti vozniki sedejo za volan brez dovoljenja in prejmejo kazen za vožnjo brez dokumentov. Spomnimo, da se avtomobilski navdušenec s svojim obvezno […]
• Rože za moške. Katere rože lahko podarite moškemu? Katere rože lahko podarite moškemu? Ni veliko »moških« rož, so pa takšne, ki jih podarimo moškim. Majhen seznam cvetja pred vami: krizanteme. Vrtnice. Nageljni. […]
• Servisni memo je posebna oblika dokumenta, ki se uporablja v notranje okolje podjetja in služi za hitro reševanje tekočih proizvodnih problemov. Običajno je ta dokument sestavljen z namenom predstavitve nekaterih […]
• Kdaj in kako prejeti kapitalski del pokojnine pri Sberbank? Sberbank je partnerska banka državnega pokojninskega sklada. Na podlagi tega bi lahko državljani, ki so se prijavili za naložbeno pokojnino, prenesli naložbeni del […]
• Otroški dodatki v Uljanovsku in Uljanovski regiji leta 2018 Poleg tega v vseh regijah delujejo programi, odobreni z zvezno zakonodajo. Poglejmo, kdo lahko računa na kakšne ugodnosti. kako regionalne oblasti […]
• Podroben vodnik o tem, kako sestaviti pooblastilo za zastopanje interesov posameznika na sodišču V civilnem ali arbitražnem zahtevku, v upravni ali kazenski zadevi lahko interese tožnika in tožene stranke zastopa odvetnik: […]

Navodila

Zapišite dani logaritemski izraz. Če izraz uporablja logaritem 10, je njegov zapis skrajšan in izgleda takole: lg b je decimalni logaritem. Če ima logaritem za osnovo število e, potem zapišimo izraz: ln b – naravni logaritem. Razume se, da je rezultat any potenca, na katero je treba dvigniti osnovno število, da dobimo število b.

Pri iskanju vsote dveh funkcij ju preprosto ločite eno za drugo in seštejte rezultate: (u+v)" = u"+v";

Pri iskanju odvoda produkta dveh funkcij je treba odvod prve funkcije pomnožiti z drugo in dodati odvod druge funkcije, pomnožen s prvo funkcijo: (u*v)" = u"*v +v"*u;

Da bi našli odvod količnika dveh funkcij, je treba od produkta odvoda dividende, pomnoženega s funkcijo delitelja, odšteti produkt odvoda delitelja, pomnoženega s funkcijo dividende, in deliti vse to s funkcijo delitelja na kvadrat. (u/v)" = (u"*v-v"*u)/v^2;

Če je dano kompleksna funkcija, potem je treba pomnožiti derivat notranja funkcija in izpeljanka zunanjega. Naj bo y=u(v(x)), potem je y"(x)=y"(u)*v"(x).

Z uporabo zgornjih rezultatov lahko ločite skoraj vsako funkcijo. Oglejmo si torej nekaj primerov:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
Težave so tudi pri izračunu izpeljanke v točki. Naj bo podana funkcija y=e^(x^2+6x+5), vrednost funkcije morate najti v točki x=1.
1) Poiščite odvod funkcije: y"=e^(x^2-6x+5)*(2*x +6).

2) Izračunaj vrednost funkcije v dano točko y"(1)=8*e^0=8

Video na temo

Koristen nasvet

Naučite se tabele elementarnih odvodov. To bo znatno prihranilo čas.

Viri:

• derivat konstante

Kakšna je torej razlika med racionalna enačba od racionalnega? Če je neznana spremenljivka pod znakom kvadratni koren, potem enačba velja za iracionalno.

Navodila

Glavna metoda za reševanje takih enačb je metoda konstruiranja obeh strani enačbe v kvadrat. Vendar. to je naravno, prva stvar, ki jo morate storiti, je, da se znebite znaka. Ta metoda tehnično ni zahtevna, včasih pa lahko povzroči težave. Na primer, enačba je v(2x-5)=v(4x-7). Če kvadrirate obe strani, dobite 2x-5=4x-7. Reševanje takšne enačbe ni težko; x=1. Toda številka 1 ne bo dana enačbe. Zakaj? V enačbo zamenjajte eno namesto vrednosti x. Desna in leva stran bosta vsebovali izraze, ki nimajo smisla, tj. Ta vrednost ni veljavna za kvadratni koren. Zato je 1 tuja korenina in zato ta enačba nima korenin.

Iracionalno enačbo torej rešimo z metodo kvadriranja obeh njenih strani. In po rešitvi enačbe je treba odrezati tuje korenine. Če želite to narediti, zamenjajte najdene korenine v prvotno enačbo.

Razmislite o drugem.
2х+vх-3=0
Seveda je to enačbo mogoče rešiti z uporabo iste enačbe kot prejšnjo. Premaknite spojine enačbe, ki nimajo kvadratnega korena, v desna stran in nato uporabite metodo kvadriranja. reši dobljeno racionalno enačbo in korene. A tudi druga, bolj elegantna. Vnesite novo spremenljivko; vх=y. V skladu s tem boste prejeli enačbo v obliki 2y2+y-3=0. Se pravi običajno kvadratna enačba. Poiščite njene korenine; y1=1 in y2=-3/2. Nato reši dva enačbe vх=1; vх=-3/2. Druga enačba nima korenin; iz prve ugotovimo, da je x=1. Ne pozabite preveriti korenin.

Reševanje identitet je povsem preprosto. Če želite to narediti, morate storiti transformacije identitete dokler cilj ni dosežen. Tako bo s pomočjo preprostih aritmetičnih operacij zastavljen problem rešen.

Boste potrebovali

• - papir;
• - pero.

Navodila

Najenostavnejša takšna preoblikovanja so algebrska skrajšana množenja (kot so kvadrat vsote (razlika), razlika kvadratov, vsota (razlika), kub vsote (razlika)). Poleg tega obstaja veliko trigonometričnih formul, ki so v bistvu enake identitete.

Dejansko je kvadrat vsote dveh členov enak kvadratu prvega plus dvakratni produkt prvega z drugim in plus kvadrat drugega, to je (a+b)^2= (a+ b)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Poenostavite oboje

Splošna načela rešitve

Ponovite iz učbenika matematične analize ali višje matematike, kaj je določen integral. Kot je znano, rešitev določen integral obstaja funkcija, katere odvod daje integrand. Ta funkcija se imenuje antiderivat. Na podlagi tega principa so zgrajeni glavni integrali.
Glede na vrsto integranda ugotovite, kateri izmed integralov tabele je v tem primeru primeren. Tega ni vedno mogoče takoj ugotoviti. Pogosto postane tabelarična oblika opazna šele po več transformacijah za poenostavitev integranda.

Metoda zamenjave spremenljivke

Če je integrand trigonometrična funkcija, katere argument je polinom, potem poskusite uporabiti metodo spremembe spremenljivk. Da bi to naredili, zamenjajte polinom v argumentu integranda z neko novo spremenljivko. Na podlagi razmerja med novimi in starimi spremenljivkami določite nove meje integracije. Z razlikovanjem tega izraza poiščite nov diferencial v . Torej boste dobili nova vrsta prejšnjega integrala, ki je blizu ali celo ustreza kateremu koli tabelarnemu.

Reševanje integralov druge vrste

Če je integral integral druge vrste, vektorska oblika integranda, potem boste morali uporabiti pravila za prehod iz teh integralov v skalarne. Eno takšnih pravil je relacija Ostrogradsky-Gauss. Ta zakon nam omogoča prehod od rotorskega fluksa določene vektorske funkcije do trojnega integrala glede na divergenco danega vektorskega polja.

Zamenjava integracijskih mej

Po najdbi protiizpeljave je treba zamenjati limite integracije. Najprej zamenjajte vrednost zgornje meje v izraz za antiizpeljavo. Dobili boste nekaj številk. Nato od dobljenega števila odštejemo drugo število, dobljeno iz spodnje meje v protiizpeljavo. Če je ena od meja integracije neskončnost, jo pri zamenjavi v antiderivativna funkcija treba je iti do meje in najti tisto, k čemur izraz stremi.
Če je integral dvodimenzionalen ali tridimenzionalen, boste morali meje integracije predstaviti geometrijsko, da boste razumeli, kako ovrednotiti integral. V primeru, recimo, tridimenzionalnega integrala, so meje integracije lahko celotne ravnine, ki omejujejo prostornino, ki se integrira.

Nadaljujemo s preučevanjem logaritmov. V tem članku bomo govorili o računanje logaritmov, se ta postopek imenuje logaritem. Najprej bomo razumeli izračun logaritmov po definiciji. Nato si poglejmo, kako se vrednosti logaritmov najdejo z uporabo njihovih lastnosti. Po tem se bomo osredotočili na izračun logaritmov skozi prvotno določene vrednosti drugih logaritmov. Na koncu se naučimo uporabljati logaritemske tabele. Celotna teorija je opremljena s primeri s podrobnimi rešitvami.

Navigacija po straneh.

Računanje logaritmov po definiciji

V najpreprostejših primerih je to mogoče izvesti precej hitro in enostavno iskanje logaritma po definiciji. Oglejmo si podrobneje, kako poteka ta proces.

Njegovo bistvo je predstaviti število b v obliki a c, iz katere je po definiciji logaritma število c vrednost logaritma. To pomeni, da po definiciji naslednja veriga enačb ustreza iskanju logaritma: log a b=log a a c =c.

Torej se izračun logaritma po definiciji zmanjša na iskanje števila c, tako da je a c = b, samo število c pa je želena vrednost logaritma.

Ob upoštevanju informacij iz prejšnjih odstavkov, ko je število pod znakom logaritma podano z določeno potenco osnove logaritma, lahko takoj navedete, čemu je logaritem enak - je enak eksponentu. Pokažimo rešitve na primerih.

Primer.

Poiščite log 2 2 −3 in izračunajte tudi naravni logaritem števila e 5,3.

rešitev.

Definicija logaritma nam omogoča, da takoj rečemo, da je log 2 2 −3 =−3. Dejansko je število pod znakom logaritma enako osnovi 2 na potenco −3.

Podobno najdemo drugi logaritem: lne 5,3 =5,3.

odgovor:

log 2 2 −3 =−3 in lne 5,3 =5,3.

Če število b pod znakom za logaritem ni določeno kot potenca osnove logaritma, potem morate skrbno pogledati, ali je možno priti do predstavitve števila b v obliki a c . Pogosto je ta predstavitev povsem očitna, zlasti kadar je število pod znakom logaritma enako osnovi na potenco 1, ali 2, ali 3, ...

Primer.

Izračunajte logaritme log 5 25 , in .

rešitev.

Preprosto je videti, da je 25=5 2, kar vam omogoča izračun prvega logaritma: log 5 25=log 5 5 2 =2.

Pojdimo k izračunu drugega logaritma. Število je mogoče predstaviti kot potenco števila 7: (poglejte, če je potrebno). torej .

Prepišimo tretji logaritem v naslednji obliki. Zdaj lahko to vidite , iz česar sklepamo, da . Zato po definiciji logaritma .

Rešitev bi lahko na kratko zapisali takole: .

odgovor:

log 5 25=2 , in .

Kadar je pod znakom za logaritem dovolj veliko naravno število, ne škodi, če ga razštejemo na prafaktorje. Pogosto pomaga, če tako število predstavimo kot neko potenco osnove logaritma in zato ta logaritem izračunamo po definiciji.

Primer.

Poiščite vrednost logaritma.

rešitev.

Nekatere lastnosti logaritmov vam omogočajo, da takoj določite vrednost logaritmov. Te lastnosti vključujejo lastnost logaritma ena in lastnost logaritma števila, ki je enako osnovi: log 1 1=log a a 0 =0 in log a a=log a a 1 =1. To pomeni, da je pod znakom logaritma številka 1 ali številka a, ki je enaka osnovi logaritma, potem sta v teh primerih logaritma enaka 0 oziroma 1.

Primer.

Čemu so enaki logaritmi in log10?

rešitev.

Ker , potem iz definicije logaritma sledi .

V drugem primeru se število 10 pod znakom za logaritem ujema s svojo osnovo, zato je decimalni logaritem desetice enak ena, to je lg10=lg10 1 =1.

odgovor:

IN lg10=1 .

Upoštevajte, da izračun logaritmov po definiciji (o katerem smo govorili v prejšnjem odstavku) implicira uporabo enakosti log a a p =p, kar je ena od lastnosti logaritmov.

V praksi, ko je število pod znakom logaritma in osnova logaritma enostavno predstavljeno kot potenca določenega števila, je zelo priročno uporabiti formulo , kar ustreza eni od lastnosti logaritmov. Oglejmo si primer iskanja logaritma, ki ponazarja uporabo te formule.

Primer.

Izračunaj logaritem.

rešitev.

odgovor:

.

Lastnosti logaritmov, ki niso omenjene zgoraj, se uporabljajo tudi pri izračunih, vendar bomo o tem govorili v naslednjih odstavkih.

Iskanje logaritmov preko drugih znanih logaritmov

Informacije v tem odstavku nadaljujejo temo uporabe lastnosti logaritmov pri njihovem izračunu. Toda tukaj je glavna razlika ta, da se lastnosti logaritmov uporabljajo za izražanje prvotnega logaritma v smislu drugega logaritma, katerega vrednost je znana. Za pojasnilo navedimo primer. Recimo, da vemo, da je log 2 3≈1,584963, potem lahko najdemo na primer log 2 6 z majhno transformacijo z uporabo lastnosti logaritma: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

V zgornjem primeru je bilo dovolj, da smo uporabili lastnost logaritma produkta. Vendar pa je veliko pogosteje potrebno uporabiti širši arzenal lastnosti logaritmov, da izračunamo prvotni logaritem preko danih.

Primer.

Izračunajte logaritem 27 na osnovo 60, če veste, da je log 60 2=a in log 60 5=b.

rešitev.

Najti moramo torej dnevnik 60 27 . Lahko vidimo, da je 27 = 3 3, prvotni logaritem pa lahko zaradi lastnosti logaritma potence prepišemo kot 3·log 60 3.

Zdaj pa poglejmo, kako izraziti log 60 3 z znanimi logaritmi. Lastnost logaritma števila, ki je enako osnovi, nam omogoča, da zapisujemo log enakosti 60 60=1. Po drugi strani pa je log 60 60=log60(2 2 3 5)= log 60 2 2 +log 60 3+log 60 5= 2·log 60 2+log 60 3+log 60 5 . torej 2 log 60 2+log 60 3+log 60 5=1. torej log 60 3=1−2·log 60 2−log 60 5=1−2·a−b.

Na koncu izračunamo prvotni logaritem: log 60 27=3 log 60 3= 3·(1−2·a−b)=3−6·a−3·b.

odgovor:

log 60 27=3·(1−2·a−b)=3−6·a−3·b.

Ločeno je treba omeniti pomen formule za prehod na novo osnovo logaritma oblike . Omogoča premik od logaritmov s katero koli osnovo do logaritmov z določeno osnovo, katerih vrednosti so znane ali jih je mogoče najti. Običajno se iz prvotnega logaritma s prehodno formulo premaknejo na logaritme v eni od osnov 2, e ali 10, saj za te baze obstajajo tabele logaritmov, ki omogočajo izračun njihovih vrednosti z določeno stopnjo natančnost. V naslednjem odstavku bomo pokazali, kako se to naredi.

Logaritemske tabele in njihova uporaba

Za približen izračun lahko uporabite vrednosti logaritmov logaritemske tabele. Najpogosteje uporabljena tabela logaritmov z bazo 2, tabela naravnih logaritmov in tabela decimalnih logaritmov. Pri delu v decimalnem številskem sistemu je priročno uporabljati tabelo logaritmov, ki temelji na osnovi deset. Z njegovo pomočjo se bomo naučili poiskati vrednosti logaritmov.

Predstavljena tabela vam omogoča, da poiščete vrednosti decimalnih logaritmov števil od 1.000 do 9.999 (s tremi decimalnimi mesti) z natančnostjo ene desettisočinke. Analizirali bomo načelo iskanja vrednosti logaritma s tabelo decimalnih logaritmov na posebnem primeru - tako je jasnejše. Poiščimo log1.256.

V levem stolpcu tabele decimalnih logaritmov najdemo prvi dve števki števila 1,256, torej najdemo 1,2 (to število je zaradi jasnosti obkroženo z modro barvo). Tretja števka števila 1.256 (številka 5) se nahaja v prvi ali zadnji vrstici levo od dvojne črte (to število je obkroženo z rdečo barvo). Četrta številka prvotnega števila 1.256 (številka 6) se nahaja v prvi ali zadnji vrstici desno od dvojne črte (to število je obkroženo z zeleno črto). Sedaj najdemo številke v celicah logaritemske tabele na presečišču označene vrstice in označenih stolpcev (te številke so označene oranžno). Vsota označenih števil daje želeno vrednost decimalnega logaritma natančno na četrto decimalno mesto, to je log1,236≈0,0969+0,0021=0,0990.

Ali je mogoče z uporabo zgornje tabele najti vrednosti decimalnih logaritmov števil, ki imajo več kot tri števke za decimalno vejico, pa tudi tistih, ki presegajo obseg od 1 do 9,999? Ja lahko. Pokažimo, kako se to naredi s primerom.

Izračunajmo lg102,76332. Najprej morate zapisati številko v standardni obliki: 102,76332=1,0276332·10 2. Po tem je treba mantiso zaokrožiti na tretjo decimalno mesto, imamo 1,0276332 10 2 ≈1,028 10 2, medtem ko je prvotni decimalni logaritem približno enak logaritmu dobljenega števila, to pomeni, da vzamemo log102,76332≈lg1,028·10 2. Zdaj uporabimo lastnosti logaritma: lg1.028·10 2 =lg1.028+lg10 2 =lg1.028+2. Nazadnje najdemo vrednost logaritma lg1,028 iz tabele decimalnih logaritmov lg1,028≈0,0086+0,0034=0,012. Kot rezultat, celoten postopek izračuna logaritma izgleda takole: log102.76332=log1.0276332 10 2 ≈lg1.028 10 2 = log1,028+lg10 2 =log1,028+2≈0,012+2=2,012.

Na koncu je treba omeniti, da lahko s tabelo decimalnih logaritmov izračunate približno vrednost katerega koli logaritma. Če želite to narediti, je dovolj, da uporabite formulo prehoda, da greste na decimalne logaritme, poiščete njihove vrednosti v tabeli in izvedete preostale izračune.

Na primer, izračunajmo log 2 3 . Po formuli za prehod na novo osnovo logaritma imamo . Iz tabele decimalnih logaritmov najdemo log3≈0,4771 in log2≈0,3010. torej .

Bibliografija.

• Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. in drugi Algebra in začetki analize: učbenik za 10.-11.
• Gusev V.A., Mordkovich A.G. Matematika (priročnik za vpisnike v tehnične šole).

Pojem logaritma in osnovna logaritemska istovetnost

Koncept logaritma in osnovna logaritemska identiteta sta tesno povezana, ker definicija logaritma v matematični zapis in je .

Osnovna logaritemska istovetnost izhaja iz definicije logaritma:

Definicija 1

Logaritem imenujejo eksponent $n$, pri povišanju na katerega dobijo števila $a$ število $b$.

Opomba 1

Eksponentna enačba$a^n=b$ za $a > 0$, $a \ne 1$ nima rešitev za nepozitivno $b$ in ima en sam koren za pozitivno $b$. Ta koren se imenuje logaritem števila $b$ na osnovo $a$ in zapiši:

$a^(\log_(a) b)=b$.

Definicija 2

Izraz

$a^(\log_(a) b)=b$

klical osnovna logaritemska identiteta pod pogojem, da je $a,b > 0$, $a \ne 1$.

Primer 1

$17^(\log_(17) 6)=6$;

$e^(\ln⁡13) =13$;

$10^(\lg23)=23$.

Osnovna logaritemska identiteta

Glavni logaritemska identiteta se imenuje zato uporablja se skoraj vedno pri delu z logaritmi. Poleg tega so z njegovo pomočjo utemeljene osnovne lastnosti logaritmov.

Primer 2

$7^5=16.807$, torej $\log_(7)16.807=5$.

$3^(-5)=\frac(1)(243)$, torej $\log_(3)\frac(1)(243)=-5$.

$11^0=1$, torej $\log_(11)⁡1=0$.

Razmislimo posledica osnovne logaritemske istovetnosti:

Definicija 3

Če sta dva logaritma z enakimi osnovami enaka, potem sta logaritemska izraza enaka:

če je $\log_(a)⁡b=\log_(a)⁡c$, potem $b=c$.

Razmislimo omejitve, ki se uporabljajo za logaritemsko identiteto:

Ker pri povišanju enote na poljubno potenco vedno dobimo eno in enakost $x=\log_(a)⁡b$ obstaja samo za $b=1$, potem bo $\log_(1)⁡1$ poljubno realno število. Da bi se izognili tej dvoumnosti, vzemite $a \ne 1$.

Logaritem za $a=0$ po definiciji lahko obstaja samo za $b=0$. Ker Ko dvignemo nič na poljubno potenco, vedno dobimo nič, potem je $\log_(0)⁡0$ lahko poljubno realno število. Da bi se izognili tej dvoumnosti, vzemite $a \ne 0$. Za $a racionalno in neracionalno logaritem vrednosti, saj stopnjo z racionalnim in iracionalnim eksponentom je mogoče izračunati samo za pozitivne baze. Če želite preprečiti to situacijo, vzemite $a > 0$.

$b > 0$ sledi iz pogoja $a > 0$, saj $x=\log_(a)⁡b$ in potenca pozitivnega števila a bo vedno pozitivna.

Osnovna logaritemska identiteta se pogosto uporablja za poenostavitev logaritemskih izrazov.

Primer 3

Izračunajte $81^(\log_(9) 7)$.

rešitev.

Za uporabo osnovne logaritemske identitete je potrebno, da sta osnova logaritma in potence enaki. Osnovo diplome zapišimo v obliki:

Zdaj lahko napišemo:

$81^(\log_(9)7)=(9^2)^(\log_(9)7)=$

Uporabimo lastnost moči:

$=9^(2 \cdot \log_(9)7)=9^(\log_(9)7) \cdot 9^(\log_(9)7)=$

osnovna logaritemska identiteta se zdaj lahko uporabi za vsak faktor:

$=7 \cdot 7=49$.

Opomba 2

Za uporabo osnovne logaritemske identitete se lahko zatečete tudi k zamenjavi osnove logaritma z izrazom, ki se pojavi pod znakom za logaritem, in obratno.

Primer 4

Izračunajte $7^(\frac(1)(\log_(11) 7))$.

rešitev.

$7^(\frac(1)(\log_(11) 7))=7^(\log_(7) 11)=11$.

Odgovori: $11$.

Primer 5

Izračunajte $7^(\frac(3)(\log_(11) 7))$.