Jak rozwiązywać znaczące ułamki zwykłe. Działania na ułamkach zwykłych, reguły, przykłady, rozwiązania

Umówmy się, że „działania na ułamkach zwykłych” na naszej lekcji będą oznaczać działania na ułamkach zwykłych. Ułamek zwykły to ułamek, który ma takie atrybuty, jak licznik, linia ułamkowa i mianownik. To odróżnia ułamek zwykły od ułamka dziesiętnego, który otrzymuje się z ułamka zwykłego poprzez zmniejszenie mianownika do wielokrotności 10. Dziesiętny zapisywane z przecinkiem oddzielającym część całkowitą od części ułamkowej. Będziemy rozmawiać o operacjach na ułamkach zwyczajnych, gdyż to one sprawiają największe trudności uczniom, którzy zapomnieli podstawy tego tematu omawianego w pierwszej połowie szkolnych zajęć z matematyki. Jednocześnie przy przekształcaniu wyrażeń w matematyce wyższej stosuje się głównie operacje na ułamkach zwykłych. Same skróty ułamkowe są tego warte! Ułamki dziesiętne nie sprawiają żadnych szczególnych trudności. Więc śmiało!

Mówi się, że dwa ułamki są równe, jeśli .

Na przykład od

Ułamki zwykłe i (since) i (since) są również równe.

Oczywiście oba ułamki i są równe. Oznacza to, że jeśli licznik i mianownik danego ułamka pomnożymy lub podzielimy przez tę samą liczbę naturalną, otrzymamy ułamek równy podanemu: .

Właściwość tę nazywa się podstawową właściwością ułamka.

Podstawową właściwość ułamka można wykorzystać do zmiany znaków licznika i mianownika ułamka. Jeśli licznik i mianownik ułamka pomnożymy przez -1, otrzymamy . Oznacza to, że wartość ułamka nie zmieni się, jeżeli jednocześnie zmienią się znaki licznika i mianownika. Jeśli zmienisz znak tylko licznika lub tylko mianownika, to ułamek zmieni swój znak:

Redukcja ułamków

Korzystając z podstawowej właściwości ułamka, możesz zamienić dany ułamek na inny ułamek równy podanemu, ale o mniejszym liczniku i mianowniku. To podstawienie nazywa się redukcją frakcji.

Niech na przykład zostanie podany ułamek. Liczby 36 i 48 mają najwięcej wspólny dzielnik 12. Następnie

Ogólnie rzecz biorąc, skrócenie ułamka jest zawsze możliwe, jeśli licznik i mianownik nie są wzajemnie liczbami pierwszymi. Jeśli licznik i mianownik są wzajemne liczby pierwsze, wówczas ułamek nazywa się nieredukowalnym.

Zatem skrócenie ułamka oznacza podzielenie licznika i mianownika ułamka przez wspólny czynnik. Wszystko powyższe dotyczy również wyrażeń ułamkowych zawierających zmienne.

Przykład 1. Zmniejsz ułamek

Rozwiązanie. Aby rozłożyć licznik na czynniki, najpierw przedstawiamy jednomian - 5 xy w sumie - 2 xy - 3xy, otrzymujemy

Aby rozłożyć mianownik na czynniki, używamy wzoru na różnicę kwadratów:

W rezultacie

Sprowadzanie ułamków do wspólnego mianownika

Niech dwa ułamki i . Mają różne mianowniki: 5 i 7. Korzystając z podstawowej właściwości ułamków, możesz zastąpić te ułamki innymi, które są im równe i takie, że powstałe ułamki będą miały te same mianowniki. Mnożąc licznik i mianownik ułamka przez 7, otrzymujemy

Mnożąc licznik i mianownik ułamka przez 5, otrzymujemy

Zatem ułamki sprowadzamy do wspólnego mianownika:

Ale to nie jedyne rozwiązanie problemu: na przykład te ułamki można również sprowadzić do wspólnego mianownika 70:

i ogólnie do dowolnego mianownika podzielnego zarówno przez 5, jak i 7.

Rozważmy inny przykład: sprowadźmy ułamki do wspólnego mianownika. Argumentując jak w poprzednim przykładzie, otrzymujemy

Ale w tym przypadku możliwe jest sprowadzenie ułamków do wspólnego mianownika, który jest mniejszy niż iloczyn mianowników tych ułamków. Znajdźmy najmniejszą wspólną wielokrotność liczb 24 i 30: LCM(24, 30) = 120.

Ponieważ 120:4 = 5, aby zapisać ułamek o mianowniku 120, należy pomnożyć zarówno licznik, jak i mianownik przez 5, liczbę tę nazywa się dodatkowym współczynnikiem. Oznacza .

Następnie otrzymujemy 120:30=4. Mnożąc licznik i mianownik ułamka przez dodatkowy współczynnik 4, otrzymujemy .

Zatem te ułamki sprowadza się do wspólnego mianownika.

Najmniejsza wspólna wielokrotność mianowników tych ułamków jest najmniejszym możliwym wspólnym mianownikiem.

Dla wyrażenia ułamkowe, które obejmują zmienne, wspólnym mianownikiem jest wielomian podzielony przez mianownik każdego ułamka.

Przykład 2. Znajdź wspólny mianownik ułamków i.

Rozwiązanie. Wspólnym mianownikiem tych ułamków jest wielomian, ponieważ jest on podzielny przez oba i. Jednak ten wielomian nie jest jedynym, który może być wspólnym mianownikiem tych ułamków. Może to być także wielomian i wielomian i wielomian itp. Zwykle przyjmują taki wspólny mianownik, że każdy inny wspólny mianownik jest dzielony przez wybrany bez reszty. Mianownik ten nazywany jest najniższym wspólnym mianownikiem.

W naszym przykładzie najniższym wspólnym mianownikiem jest . Dostał:

;

Udało nam się sprowadzić ułamki do najniższego wspólnego mianownika. Nastąpiło to poprzez pomnożenie licznika i mianownika pierwszego ułamka przez , a licznik i mianownik drugiego ułamka przez . Wielomiany nazywane są dodatkowymi czynnikami, odpowiednio dla pierwszego i drugiego ułamka.

Dodawanie i odejmowanie ułamków

Dodawanie frakcji definiuje się następująco:

Na przykład,

Jeśli B = D, To

Oznacza to, że aby dodać ułamki o tym samym mianowniku, wystarczy dodać liczniki, a mianownik pozostawić bez zmian. Na przykład,

Jeśli dodasz ułamki za pomocą różne mianowniki, następnie zwykle redukują ułamki do najniższego wspólnego mianownika, a następnie dodają liczniki. Na przykład,

Przyjrzyjmy się teraz przykładowi dodawania wyrażeń ułamkowych ze zmiennymi.

Przykład 3. Zamień wyrażenie na jeden ułamek

Rozwiązanie. Znajdźmy najniższy wspólny mianownik. Aby to zrobić, najpierw rozkładamy mianowniki na czynniki.

Licznik i to, co jest dzielone przez, jest mianownikiem.

Aby zapisać ułamek, najpierw wpisz licznik, następnie narysuj poziomą linię pod liczbą i wpisz mianownik pod tą linią. Linię poziomą oddzielającą licznik od mianownika nazywa się linią ułamkową. Czasami jest przedstawiany jako ukośny „/” lub „∕”. W takim przypadku licznik jest zapisywany po lewej stronie linii, a mianownik po prawej stronie. Na przykład ułamek „dwie trzecie” zostanie zapisany jako 2/3. Dla jasności licznik jest zwykle zapisywany na górze linii, a mianownik na dole, czyli zamiast 2/3 można znaleźć: ⅔.

Aby obliczyć iloczyn ułamków, najpierw pomnóż licznik przez jeden ułamki do licznika jest inny. Wynik zapisz w liczniku nowego ułamki. Następnie pomnóż mianowniki. Wprowadź całkowitą wartość w nowym ułamki. Na przykład 1/3? 1/5 = 1/15 (1 × 1 = 1; 3 × 5 = 15).

Aby podzielić ułamek przez drugi, należy najpierw pomnożyć licznik pierwszego przez mianownik drugiego. Zrób to samo z drugim ułamkiem (dzielnikiem). Lub przed wykonaniem wszystkich czynności najpierw „odwróć” dzielnik, jeśli jest to dla Ciebie wygodniejsze: mianownik powinien pojawić się zamiast licznika. Następnie pomnóż mianownik dywidendy przez nowy mianownik dzielnika i pomnóż liczniki. Na przykład 1/3: 1/5 = 5/3 = 1 2/3 (1 ? 5 = 5; 3 ? 1 = 3).

Źródła:

Podstawowe problemy ułamkowe

Liczby ułamkowe można wyrazić w w różnych formach dokładna wartość ilości. Na ułamkach zwykłych możesz wykonywać te same operacje matematyczne, co na liczbach całkowitych: odejmowanie, dodawanie, mnożenie i dzielenie. Aby nauczyć się decydować ułamki, musimy pamiętać o niektórych ich cechach. Zależą od rodzaju ułamki, obecność części całkowitej, wspólny mianownik. Niektóre operacje arytmetyczne wymagają zmniejszenia części ułamkowej wyniku po wykonaniu.

Będziesz potrzebować

- kalkulator

Instrukcje

Przyjrzyj się uważnie liczbom. Jeśli wśród ułamków zwykłych znajdują się ułamki dziesiętne i nieregularne, czasami wygodniej jest najpierw wykonać operacje na ułamkach dziesiętnych, a następnie przekształcić je do postaci nieregularnej. Możesz przetłumaczyć ułamki początkowo w tej formie, zapisując wartość po przecinku w liczniku i wstawiając 10 w mianowniku. Jeśli to konieczne, zmniejsz ułamek, dzieląc liczby powyżej i poniżej przez jeden dzielnik. Ułamki, w których wyodrębniona jest cała część, należy przekształcić do niewłaściwej postaci, mnożąc ją przez mianownik i dodając licznik do wyniku. Podana wartość stanie się nowym licznikiem ułamki. Aby wybrać całą część z początkowo nieprawidłowej ułamki, musisz podzielić licznik przez mianownik. Zapisz cały wynik z ułamki. A pozostała część dzielenia stanie się nowym licznikiem i mianownikiem ułamki to się nie zmienia. W przypadku ułamków zawierających część całkowitą możliwe jest wykonanie działań oddzielnie, najpierw dla liczby całkowitej, a następnie dla części ułamkowych. Na przykład można obliczyć sumę 1 2/3 i 2 ¾:
- Zamiana ułamków zwykłych na niewłaściwą formę:
- 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
- Sumowanie oddzielnie części całkowitych i ułamkowych terminów:
- 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾) = 3 +(8/12 + 9/12) = 3 + 12/17 = 3 + 1 5/12 = 4 5 /12.

Przepisz je, używając separatora „:” i kontynuuj normalny podział.

Aby uzyskać wynik końcowy, zmniejsz uzyskany ułamek, dzieląc licznik i mianownik przez jedną liczbę całkowitą, w tym przypadku największą możliwą. W tym przypadku powyżej i poniżej linii muszą znajdować się liczby całkowite.

notatka

Nie wykonuj działań arytmetycznych na ułamkach, których mianowniki są różne. Wybierz taką liczbę, że pomnożenie przez nią licznika i mianownika każdego ułamka spowoduje, że mianowniki obu ułamków będą równe.

Pomocna rada

Podczas nagrywania liczby ułamkowe Dywidenda jest zapisana powyżej linii. Ilość tę wyznacza się jako licznik ułamka. Dzielnik lub mianownik ułamka zapisuje się pod linią. Na przykład półtora kilograma ryżu jako ułamek zostanie zapisane w następujący sposób: 1 ½ kg ryżu. Jeśli mianownik ułamka wynosi 10, ułamek ten nazywa się dziesiętnym. W tym przypadku licznik (dywidenda) wpisuje się po prawej stronie całej części, oddzielając przecinkiem: 1,5 kg ryżu. Dla ułatwienia obliczeń taki ułamek zawsze można zapisać w niewłaściwej formie: 1 2/10 kg ziemniaków. Dla uproszczenia możesz zmniejszyć wartości licznika i mianownika, dzieląc je przez jedną liczbę całkowitą. W tym przykładzie możesz podzielić przez 2. Otrzymasz 1 1/5 kg ziemniaków. Upewnij się, że liczby, na których będziesz wykonywać arytmetykę, są przedstawione w tej samej formie.

Ułamki zwykłe to zwykłe liczby, które można także dodawać i odejmować. Ale ze względu na to, że zawierają mianownik, więcej skomplikowane zasady niż dla liczb całkowitych.

Rozważmy najprostszy przypadek, gdy istnieją dwie frakcje same mianowniki. Następnie:

Aby dodać ułamki o tych samych mianownikach, należy dodać ich liczniki i pozostawić mianownik bez zmian.

Aby odjąć ułamki o tych samych mianownikach, należy odjąć licznik drugiego ułamka od licznika pierwszego ułamka i ponownie pozostawić mianownik bez zmian.

W każdym wyrażeniu mianowniki ułamków są równe. Z definicji dodawania i odejmowania ułamków otrzymujemy:

Jak widać, nie jest to nic skomplikowanego: po prostu dodajemy lub odejmujemy liczniki i gotowe.

Ale nawet w tak prostych działaniach ludziom udaje się popełniać błędy. Najczęściej zapomina się, że mianownik się nie zmienia. Na przykład, dodając je, zaczynają się one również sumować, co jest zasadniczo błędne.

Pozbyć się zły nawyk Dodawanie mianowników jest dość proste. Spróbuj tego samego podczas odejmowania. W efekcie mianownik wyniesie zero, a ułamek (nagle!) straci swoje znaczenie.

Dlatego pamiętajcie raz na zawsze: podczas dodawania i odejmowania mianownik się nie zmienia!

Wiele osób popełnia również błędy przy dodawaniu kilku ułamków ujemnych. Istnieje zamieszanie ze znakami: gdzie umieścić minus i gdzie umieścić plus.

Ten problem jest również bardzo łatwy do rozwiązania. Wystarczy pamiętać, że minus przed znakiem ułamka zawsze można przenieść na licznik - i odwrotnie. I oczywiście nie zapomnij o dwóch prostych zasadach:

Plus przez minus daje minus;
Dwa minusy dają odpowiedź twierdzącą.

Spójrzmy na to wszystko na konkretnych przykładach:

Zadanie. Znajdź znaczenie wyrażenia:

W pierwszym przypadku wszystko jest proste, ale w drugim dodajmy minusy do liczników ułamków:

Co zrobić, jeśli mianowniki są różne

Nie można bezpośrednio dodawać ułamków o różnych mianownikach. Przynajmniej mi ta metoda nie jest znana. Jednak oryginalne ułamki zawsze można przepisać tak, aby mianowniki stały się takie same.

Istnieje wiele sposobów konwertowania ułamków zwykłych. Trzy z nich omówiono na lekcji „Sprowadzanie ułamków do wspólnego mianownika”, więc nie będziemy się nad nimi tutaj rozwodzić. Spójrzmy na kilka przykładów:

Zadanie. Znajdź znaczenie wyrażenia:

W pierwszym przypadku ułamki sprowadzamy do wspólnego mianownika metodą „na krzyż”. W drugim będziemy szukać NOC. Zauważ, że 6 = 2 · 3; 9 = 3 · 3. Ostatnie czynniki w tych rozwinięciach są równe, a pierwsze są względnie pierwsze. Zatem LCM(6, 9) = 2 3 3 = 18.

Co zrobić, jeśli ułamek ma część całkowitą

Mogę cię zadowolić: posiadanie różnych mianowników w ułamkach nie jest najważniejsze wielkie zło. Znacznie więcej błędów pojawia się, gdy w dodanych ułamkach zaznaczona jest cała część.

Oczywiście istnieją własne algorytmy dodawania i odejmowania takich ułamków, ale są one dość złożone i wymagają długich badań. Lepiej skorzystaj z prostego schematu poniżej:

Zamień wszystkie ułamki zwykłe zawierające część całkowitą na niewłaściwe. Otrzymujemy wyrazy normalne (nawet o różnych mianownikach), które obliczamy według zasad omówionych powyżej;
Właściwie oblicz sumę lub różnicę powstałych ułamków. W rezultacie praktycznie znajdziemy odpowiedź;
Jeśli to wszystko, co było wymagane w zadaniu, wykonujemy transformację odwrotną, tj. Ułamek niewłaściwy pozbywamy się podświetlając całą część.

Zasady przejścia do ułamki niewłaściwe i wyróżnianie całej części opisano szczegółowo w lekcji „Co to jest ułamek liczbowy”. Jeśli nie pamiętasz, koniecznie powtórz. Przykłady:

Zadanie. Znajdź znaczenie wyrażenia:

Tutaj wszystko jest proste. Mianowniki w każdym wyrażeniu są równe, więc pozostaje tylko zamienić wszystkie ułamki zwykłe na niewłaściwe i policzyć. Mamy:

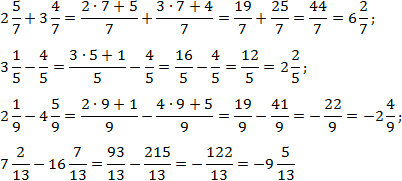
Aby uprościć obliczenia, w ostatnich przykładach pominąłem kilka oczywistych kroków.

Mała uwaga odnośnie dwóch ostatnich przykładów, gdzie odejmowane są ułamki z zaznaczoną częścią całkowitą. Minus przed drugim ułamkiem oznacza, że odejmowany jest cały ułamek, a nie tylko jego część.

Przeczytaj jeszcze raz to zdanie, spójrz na przykłady i pomyśl o tym. Tutaj początkujący popełniają ogromną liczbę błędów. Uwielbiają zlecać takie zadania testy. Spotkasz je także kilka razy w testach do tej lekcji, które zostaną wkrótce opublikowane.

Podsumowanie: ogólny schemat obliczeń

Podsumowując, dam algorytm ogólny, które pomogą Ci znaleźć sumę lub różnicę dwóch lub więcej ułamków:

Jeśli jeden lub więcej ułamków ma część całkowitą, zamień te ułamki na niewłaściwe;
Doprowadź wszystkie ułamki do wspólnego mianownika w dowolny dogodny dla ciebie sposób (chyba że oczywiście zrobili to autorzy problemów);
Dodaj lub odejmij powstałe liczby zgodnie z zasadami dodawania i odejmowania ułamków o podobnych mianownikach;
Jeśli to możliwe, skróć wynik. Jeśli ułamek jest nieprawidłowy, wybierz całą część.

Pamiętaj, że lepiej zaznaczyć całą część na samym końcu zadania, bezpośrednio przed zapisaniem odpowiedzi.

Kalkulator ułamków przeznaczony do szybkiego obliczania operacji na ułamkach zwykłych, pomoże Ci w łatwy sposób dodawać, mnożyć, dzielić czy odejmować ułamki zwykłe.

Współcześni uczniowie rozpoczynają naukę ułamków zwykłych już w piątej klasie, a ćwiczenia z nimi stają się z roku na rok coraz bardziej skomplikowane. Pojęcia i wielkości matematyczne, których uczymy się w szkole, rzadko kiedy mogą nam się przydać w życiu. dorosłe życie. Jednak ułamki, w przeciwieństwie do logarytmów i potęg, występują dość często w życiu codziennym (mierzenie odległości, ważenie towarów itp.). Nasz kalkulator przeznaczony jest do szybkich operacji na ułamkach zwykłych.

Najpierw zdefiniujmy, czym są ułamki i jakie są. Ułamki to stosunek jednej liczby do drugiej; jest to liczba składająca się z całkowitej liczby ułamków jednostki.

Rodzaje frakcji:

Zwykły
Dziesiętny
Mieszany

Przykład zwykłe ułamki:

Górna wartość to licznik, dolna to mianownik. Myślnik pokazuje nam, że górna liczba jest podzielna przez dolną liczbę. Zamiast tego formatu zapisu, gdy myślnik jest poziomy, można pisać inaczej. Możesz umieścić nachyloną linię, na przykład:

1/2, 3/7, 19/5, 32/8, 10/100, 4/1

Dziesiętne to najpopularniejszy rodzaj ułamków zwykłych. Składają się z części całkowitej i części ułamkowej, oddzielonych przecinkiem.

Przykład ułamków dziesiętnych:

0,2 lub 6,71 lub 0,125

Składa się z liczby całkowitej i części ułamkowej. Aby poznać wartość tego ułamka, musisz dodać liczbę całkowitą i ułamek.

Przykład frakcji mieszanych:

Kalkulator ułamków na naszej stronie jest w stanie szybko wykonać dowolne operacje matematyczne na ułamkach online:

Dodatek
Odejmowanie
Mnożenie
Dział

Aby przeprowadzić obliczenia, należy wpisać liczby w polach i wybrać akcję. W przypadku ułamków należy wypełnić licznik i mianownik, nie można zapisać całej liczby (jeśli ułamek jest zwyczajny). Nie zapomnij kliknąć przycisku „równe”.

Wygodne jest to, że kalkulator natychmiast zapewnia proces rozwiązywania przykładu z ułamkami, a nie tylko gotową odpowiedź. To dzięki szczegółowemu rozwiązaniu możesz wykorzystać ten materiał przy rozwiązywaniu problemów szkolnych i do celów lepszy rozwój pokryty materiał.

Należy wykonać przykładowe obliczenia:

Po wpisaniu wskaźników w pola formularza otrzymujemy:

Aby dokonać własnej kalkulacji wpisz dane w formularzu.

Kalkulator ułamków

Wpisz dwa ułamki:

		+ - * :

Powiązane sekcje.

Jeśli więc wyrażenie liczbowe składa się z liczb oraz znaków +, −, · i:, to w kolejności od lewej do prawej należy najpierw wykonać mnożenie i dzielenie, a następnie dodawanie i odejmowanie, co pozwoli znaleźć żądaną wartość wyrażenia.

Podajmy kilka przykładów dla wyjaśnienia.

Przykład.

Oblicz wartość wyrażenia 14−2·15:6−3.

Rozwiązanie.

Aby znaleźć wartość wyrażenia, należy wykonać wszystkie określone w nim czynności, zgodnie z przyjętą kolejnością wykonywania tych czynności. Najpierw w kolejności od lewej do prawej wykonujemy mnożenie i dzielenie, otrzymujemy 14−2·15:6−3=14−30:6−3=14−5−3. Teraz wykonujemy także pozostałe czynności w kolejności od lewej do prawej: 14−5−3=9−3=6. W ten sposób znaleźliśmy wartość pierwotnego wyrażenia, jest ona równa 6.

Odpowiedź:

14−2·15:6−3=6.

Przykład.

Znajdź znaczenie wyrażenia.

Rozwiązanie.

W tym przykładzie najpierw musimy wykonać mnożenie 2·(−7) i dzielenie z mnożeniem w wyrażeniu . Pamiętając jak , znajdujemy 2·(−7)=−14. I najpierw wykonaj działania zawarte w wyrażeniu , Następnie i wykonaj: .

Otrzymane wartości podstawiamy do pierwotnego wyrażenia: .

Ale co, jeśli pod znakiem pierwiastka znajduje się wyrażenie liczbowe? Aby uzyskać wartość takiego pierwiastka, należy najpierw znaleźć wartość wyrażenia radykalnego, zachowując przyjętą kolejność wykonywania czynności. Na przykład, .

W wyrażeniach liczbowych pierwiastki należy postrzegać jako pewne liczby i wskazane jest natychmiastowe zastąpienie pierwiastków ich wartościami, a następnie znalezienie wartości wynikowego wyrażenia bez pierwiastków, wykonując czynności w przyjętej kolejności.

Przykład.

Znajdź znaczenie wyrażenia z pierwiastkami.

Rozwiązanie.

Najpierw znajdźmy wartość pierwiastka . Aby to zrobić, najpierw obliczamy wartość radykalnego wyrażenia, które mamy −2·3−1+60:4=−6−1+15=8. Po drugie, znajdujemy wartość pierwiastka.

Teraz obliczmy wartość drugiego pierwiastka z pierwotnego wyrażenia: .

Wreszcie możemy znaleźć znaczenie pierwotnego wyrażenia, zastępując rdzenie ich znaczeniami: .

Odpowiedź:

Dość często, aby znaleźć znaczenie wyrażenia z korzeniami, należy je najpierw przekształcić. Pokażmy rozwiązanie przykładu.

Przykład.

Jakie jest znaczenie wyrażenia .

Rozwiązanie.

Pierwiastka z trzech nie jesteśmy w stanie zastąpić jego dokładną wartością, co nie pozwala na obliczenie wartości tego wyrażenia w sposób opisany powyżej. Możemy jednak obliczyć wartość tego wyrażenia, wykonując proste przekształcenia. Odpowiedni wzór na różnicę kwadratową: . Biorąc pod uwagę , otrzymujemy . Zatem wartość pierwotnego wyrażenia wynosi 1.

Odpowiedź:

Ze stopniami

Jeżeli podstawą i wykładnikiem są liczby, to ich wartość oblicza się poprzez określenie stopnia, np. 3 2 =3·3=9 lub 8 −1 =1/8. Istnieją również wpisy, w których podstawa i/lub wykładnik są pewnymi wyrażeniami. W takich przypadkach należy znaleźć wartość wyrażenia w podstawie, wartość wyrażenia w wykładniku, a następnie obliczyć wartość samego stopnia.

Przykład.

Znajdź wartość wyrażenia za pomocą potęg formy 2 3·4−10 +16·(1−1/2) 3,5−2·1/4.

Rozwiązanie.

W oryginalnym wyrażeniu występują dwie potęgi 2 3,4−10 i (1−1/2) 3,5−2,1/4. Ich wartości należy obliczyć przed wykonaniem innych czynności.

Zacznijmy od potęgi 2 3,4−10. Jego wskaźnik zawiera wyrażenie liczbowe, obliczmy jego wartość: 3,4−10=12−10=2. Teraz możesz znaleźć wartość samego stopnia: 2 3·4−10 =2 2 =4.

Podstawa i wykładnik (1−1/2) 3,5−2 1/4 zawierają wyrażenia, obliczamy ich wartości, aby następnie znaleźć wartość wykładnika. Mamy (1−1/2) 3,5−2 1/4 =(1/2) 3 =1/8.

Teraz wracamy do pierwotnego wyrażenia, zastępujemy zawarte w nim stopnie ich wartościami i znajdujemy wartość potrzebnego wyrażenia: 2 3·4−10 +16·(1−1/2) 3,5−2·1/4 = 4+16·1/8=4+2=6.

Odpowiedź:

2 3·4−10 +16·(1−1/2) 3,5−2·1/4 =6.

Warto zauważyć, że zdarzają się częstsze przypadki, w których wskazane jest przeprowadzenie wstępnego badania uproszczenie wyrażeń za pomocą potęg na bazie .

Przykład.

Znajdź znaczenie wyrażenia .

Rozwiązanie.

Sądząc po wykładnikach w tym wyrażeniu, uzyskanie dokładnych wartości wykładników nie będzie możliwe. Spróbujmy uprościć oryginalne wyrażenie, może to pomoże znaleźć jego znaczenie. Mamy

Odpowiedź:

Potęgi w wyrażeniach często idą w parze z logarytmami, ale porozmawiamy o znalezieniu znaczenia wyrażeń z logarytmami w jednym z nich.

Znajdowanie wartości wyrażenia za pomocą ułamków zwykłych

Wyrażenia numeryczne mogą zawierać ułamki w swoim zapisie. Jeśli chcesz znaleźć znaczenie takiego wyrażenia, ułamki inne niż ułamki należy zastąpić ich wartościami, zanim przejdziesz do pozostałych kroków.

Licznik i mianownik ułamków zwykłych (które różnią się od zwykłych ułamków) mogą zawierać zarówno niektóre liczby, jak i wyrażenia. Aby obliczyć wartość takiego ułamka, należy obliczyć wartość wyrażenia w liczniku, obliczyć wartość wyrażenia w mianowniku, a następnie obliczyć wartość samego ułamka. Porządek ten tłumaczy się faktem, że ułamek a/b, gdzie aib są pewnymi wyrażeniami, zasadniczo reprezentuje iloraz postaci (a):(b), ponieważ .

Spójrzmy na przykładowe rozwiązanie.

Przykład.

Znajdź znaczenie wyrażenia z ułamkami zwykłymi .

Rozwiązanie.

W oryginalnym wyrażeniu liczbowym znajdują się trzy ułamki I . Aby znaleźć wartość pierwotnego wyrażenia, musimy najpierw zastąpić te ułamki ich wartościami. Zróbmy to.

Licznik i mianownik ułamka zawierają liczby. Aby znaleźć wartość takiego ułamka, zamień kreskę ułamkową na znak dzielenia i wykonaj tę czynność: .

W liczniku ułamka znajduje się wyrażenie 7−2·3, którego wartość łatwo znaleźć: 7−2·3=7−6=1. Zatem, . Możesz przystąpić do znajdowania wartości trzeciego ułamka.

Trzeci ułamek w liczniku i mianowniku zawiera wyrażenia liczbowe, dlatego najpierw musisz obliczyć ich wartości, a to pozwoli ci znaleźć wartość samego ułamka. Mamy .

Pozostaje zastąpić znalezione wartości oryginalnym wyrażeniem i wykonać pozostałe czynności: .

Odpowiedź:

Często, szukając wartości wyrażeń z ułamkami, trzeba wykonać upraszczanie wyrażeń ułamkowych, polegające na wykonywaniu operacji na ułamkach i redukowaniu ułamków.

Przykład.

Znajdź znaczenie wyrażenia .

Rozwiązanie.

Pierwiastka z pięciu nie da się całkowicie wyodrębnić, dlatego aby znaleźć wartość pierwotnego wyrażenia, najpierw je uprośćmy. Dla tego pozbądźmy się irracjonalności w mianowniku pierwszy ułamek: . Następnie oryginalne wyrażenie przyjmie formę . Po odjęciu ułamków pierwiastki znikną, co pozwoli nam znaleźć wartość pierwotnie podanego wyrażenia: .

Odpowiedź:

Z logarytmami

Jeśli wyrażenie numeryczne zawiera i jeśli można się ich pozbyć, należy to zrobić przed wykonaniem innych czynności. Na przykład, znajdując wartość wyrażenia log 2 4+2·3, logarytm log 2 4 zastępuje się jego wartością 2, po czym pozostałe czynności są wykonywane w zwykłej kolejności, czyli log 2 4+2 ·3=2+2·3=2 +6=8.

Jeżeli pod znakiem logarytmu i/lub u jego podstawy znajdują się wyrażenia liczbowe, najpierw ustalane są ich wartości, po czym obliczana jest wartość logarytmu. Rozważmy na przykład wyrażenie z logarytmem w postaci . U podstawy logarytmu i pod jego znakiem znajdują się wyrażenia liczbowe, znajdujemy ich wartości: . Teraz znajdujemy logarytm, po czym kończymy obliczenia: .

Jeśli logarytmy nie są obliczane dokładnie, należy je wstępnie uprościć za pomocą . W takim przypadku konieczna jest dobra znajomość materiału artykułu konwertowanie wyrażeń logarytmicznych.

Przykład.

Znajdź wartość wyrażenia za pomocą logarytmów .

Rozwiązanie.

Zacznijmy od obliczenia log 2 (log 2 256) . Ponieważ 256=2 · 8, to log 2 · 256=8, zatem log 2 (log 2 256) = log 2 8 = log 2 2 3 =3.

Logarytmy log 6 2 i log 6 3 można pogrupować. Suma dziennik logarytmów 6 2+log 6 3 równa się logarytmowi iloczynu log 6 (2 3), zatem log 6 2+log 6 3=log 6 (2 3)=log 6 6=1.

Teraz spójrzmy na ułamek. Na początek przepiszemy podstawę logarytmu w mianowniku w postaci ułamka zwykłego na 1/5, po czym skorzystamy z właściwości logarytmów, co pozwoli nam uzyskać wartość ułamka:
.

Pozostaje tylko zastąpić otrzymane wyniki oryginalnym wyrażeniem i dokończyć znajdowanie jego wartości:

Odpowiedź:

Jak znaleźć wartość wyrażenia trygonometrycznego?

Gdy wyrażenie liczbowe zawiera lub itp., ich wartości są obliczane przed wykonaniem innych czynności. Jeśli pod znakiem funkcji trygonometrycznych znajdują się wyrażenia liczbowe, najpierw obliczane są ich wartości, po czym znajdują się wartości funkcji trygonometrycznych.

Przykład.

Znajdź znaczenie wyrażenia .

Rozwiązanie.

Wracając do artykułu, otrzymujemy i cosπ=−1 . Zastępujemy te wartości oryginalnym wyrażeniem, przyjmuje ono formę . Aby znaleźć jego wartość, należy najpierw wykonać potęgowanie, a następnie zakończyć obliczenia: .

Odpowiedź:

Warto zauważyć, że obliczanie wartości wyrażeń za pomocą sinusów, cosinusów itp. często wymaga wcześniejszego konwertowanie wyrażenia trygonometrycznego.

Przykład.

Jaka jest wartość wyrażenia trygonometrycznego .

Rozwiązanie.

Przekształćmy oryginalne wyrażenie za pomocą , w tym przypadku będziemy potrzebować wzoru na cosinus podwójnego kąta i wzoru na sumę cosinusów:

Przekształcenia, których dokonaliśmy, pomogły nam znaleźć znaczenie wyrażenia.

Odpowiedź:

Sprawa ogólna

Ogólnie rzecz biorąc, wyrażenie liczbowe może zawierać pierwiastki, potęgi, ułamki, niektóre funkcje i nawiasy. Znalezienie wartości takich wyrażeń polega na działaniu następne kroki:

pierwsze pierwiastki, potęgi, ułamki itp. są zastępowane przez ich wartości,
dalsze działania w nawiasach,
i w kolejności od lewej do prawej wykonywane są pozostałe operacje - mnożenie i dzielenie, a następnie dodawanie i odejmowanie.

Wymienione działania są wykonywane aż do uzyskania końcowego wyniku.

Przykład.

Znajdź znaczenie wyrażenia .

Rozwiązanie.

Forma tego wyrażenia jest dość złożona. W tym wyrażeniu widzimy ułamki zwykłe, pierwiastki, potęgi, sinusy i logarytmy. Jak znaleźć jego wartość?

Przechodząc przez zapis od lewej do prawej, natrafiamy na ułamek formy . Wiemy, że pracując z ułamkami złożonymi, musimy osobno obliczyć wartość licznika, osobno mianownik i na koniec znaleźć wartość ułamka.

W liczniku mamy pierwiastek formy . Aby określić jego wartość, należy najpierw obliczyć wartość wyrażenia radykalnego . Jest tu sinus. Jego wartość możemy znaleźć dopiero po obliczeniu wartości wyrażenia . To możemy zrobić: . Zatem skąd i skąd .

Mianownik jest prosty: .

Zatem, .

Po podstawieniu tego wyniku do pierwotnego wyrażenia przyjmie ono postać . Wynikowe wyrażenie zawiera stopień . Aby znaleźć jego wartość, musimy najpierw znaleźć wartość wskaźnika, który mamy .

Więc, .

Odpowiedź:

Jeśli nie jest możliwe obliczenie dokładnych wartości pierwiastków, potęg itp., można spróbować się ich pozbyć za pomocą pewnych przekształceń, a następnie powrócić do obliczania wartości według określonego schematu.

Racjonalne sposoby obliczania wartości wyrażeń

Obliczanie wartości wyrażeń numerycznych wymaga konsekwencji i dokładności. Tak, konieczne jest przestrzeganie sekwencji działań opisanych w poprzednich akapitach, ale nie ma potrzeby robić tego na ślepo i mechanicznie. Mamy przez to na myśli to, że często można zracjonalizować proces znajdowania znaczenia wyrażenia. Na przykład pewne właściwości operacji na liczbach mogą znacznie przyspieszyć i uprościć znajdowanie wartości wyrażenia.

Znamy na przykład tę właściwość mnożenia: jeśli jeden z czynników w iloczynie jest równy zero, to wartość iloczynu jest równa zero. Korzystając z tej właściwości, możemy od razu powiedzieć, że wartość wyrażenia 0·(2·3+893−3234:54·65−79·56·2,2)·(45·36−2·4+456:3·43) jest równe zero. Gdybyśmy postępowali według standardowej kolejności działań, musielibyśmy najpierw obliczyć wartości uciążliwych wyrażeń w nawiasach, co zajęłoby dużo czasu, a wynik i tak byłby zerowy.

Wygodne jest również skorzystanie z właściwości odejmowania równe liczby: Jeśli od liczby odejmiesz taką samą liczbę, wynikiem będzie zero. Tę właściwość można rozpatrywać szerzej: różnica między dwoma identycznymi wyrażeniami liczbowymi wynosi zero. Na przykład, bez obliczania wartości wyrażeń w nawiasach, możesz znaleźć wartość wyrażenia (54 6−12 47362:3)−(54 6−12 47362:3), jest równa zeru, ponieważ pierwotne wyrażenie jest różnicą identycznych wyrażeń.

Transformacje tożsamości mogą ułatwić racjonalne obliczenie wartości wyrażeń. Przydatne może być na przykład grupowanie terminów i czynników; nie mniej często stosuje się umieszczanie wspólnego czynnika w nawiasach. Zatem wartość wyrażenia 53,5+53,7-53,11+5 jest bardzo łatwa do znalezienia po usunięciu współczynnika 53 z nawiasów: 53·(5+7−11)+5=53·1+5=53+5=58. Bezpośrednie obliczenia trwałyby znacznie dłużej.

Podsumowując ten punkt, zwróćmy uwagę na racjonalne podejście do obliczania wartości wyrażeń z ułamkami - identyczne czynniki w liczniku i mianowniku ułamka są anulowane. Na przykład redukując te same wyrażenia w liczniku i mianowniku ułamka pozwala od razu znaleźć jego wartość, która jest równa 1/2.

Znajdowanie wartości wyrażenia dosłownego i wyrażenia ze zmiennymi

Wartość wyrażenia dosłownego i wyrażenia ze zmiennymi znajduje się dla określonych podanych wartości liter i zmiennych. Oznacza to, że mówimy o znalezieniu wartości wyrażenia dosłownego dla podanych wartości liter lub o znalezieniu wartości wyrażenia ze zmiennymi dla wybranych wartości zmiennych.

Reguła znalezienie wartości wyrażenia literałowego lub wyrażenia ze zmiennymi dla podanych wartości liter lub wybranych wartości zmiennych wygląda następująco: należy podstawić podane wartości liter lub zmiennych do wyrażenia pierwotnego i obliczyć wartość wynikowy wyrażenie numeryczne, jest to pożądana wartość.

Przykład.

Oblicz wartość wyrażenia 0,5·x−y przy x=2,4 i y=5.

Rozwiązanie.

Aby znaleźć wymaganą wartość wyrażenia, należy najpierw podstawić podane wartości zmiennych do pierwotnego wyrażenia, a następnie wykonać następujące kroki: 0,5·2,4−5=1,2−5=−3,8.

Odpowiedź:

−3,8 .

Na koniec, czasami wykonanie konwersji wyrażeń literałowych i zmiennych da ich wartości, niezależnie od wartości liter i zmiennych. Na przykład wyrażenie x+3−x można uprościć, po czym przyjmie ono postać 3. Z tego możemy wywnioskować, że wartość wyrażenia x+3−x jest równa 3 dla dowolnych wartości zmiennej x z jej zakresu wartości dopuszczalnych (APV). Inny przykład: wartość wyrażenia jest równa 1 dla wszystkich dodatnich wartości x, więc zakres dopuszczalnych wartości zmiennej x w oryginalnym wyrażeniu jest zbiorem liczb dodatnich i w tym zakresie równość trzyma.

Bibliografia.

Matematyka: podręcznik dla 5 klasy. ogólne wykształcenie instytucje / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - wyd. 21, skreślone. - M.: Mnemosyne, 2007. - 280 s.: il. ISBN 5-346-00699-0.
Matematyka. Klasa 6: edukacyjna. dla edukacji ogólnej instytucje / [N. Tak, Vilenkin i inni]. - wyd. 22, wyd. - M.: Mnemosyne, 2008. - 288 s.: il. ISBN 978-5-346-00897-2.
Algebra: podręcznik dla 7 klasy ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 17. - M.: Edukacja, 2008. - 240 s. : chory. - ISBN 978-5-09-019315-3.
Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
Algebra: Klasa 9: edukacyjna. dla edukacji ogólnej instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2009. - 271 s. : chory. - ISBN 978-5-09-021134-5.
Algebra i początek analizy: Proc. dla klas 10-11. ogólne wykształcenie instytucje / A. N. Kołmogorow, A. M. Abramov, Yu. P. Dudnitsyn i inni; wyd. A. N. Kołmogorowa - wyd. 14 - M.: Edukacja, 2004. - 384 s.: chory - ISBN 5-09-013651-3.