Zaloguj się według bazy. Definicja logarytmu i jego własności: teoria i rozwiązywanie problemów

(z greckiego λόγος - „słowo”, „relacja” i ἀριθμός - „liczba”) liczby B z powodu A(logarytm α B) nazywa się taką liczbą C, I B= c, czyli log α B=C I b=aC są równoważne. Logarytm ma sens, jeśli a > 0, a ≠ 1, b > 0.

Innymi słowy logarytm liczby B z powodu A sformułowany jako wykładnik, do którego należy podnieść liczbę A aby uzyskać numer B(logarytm istnieje tylko dla liczb dodatnich).

Z tego sformułowania wynika, że ​​obliczenie x= log α B, jest równoważne rozwiązaniu równania a x = b.

Na przykład:

log 2 8 = 3, ponieważ 8 = 2 3 .

Zauważamy, że wskazane sformułowanie logarytmu umożliwia natychmiastowe określenie wartość logarytmu gdy liczba pod znakiem logarytmu jest pewną potęgą podstawy. Rzeczywiście, sformułowanie logarytmu umożliwia uzasadnienie, że jeśli b=a do, a następnie logarytm liczby B z powodu A równa się Z. Oczywiste jest również, że temat logarytmu jest ściśle związany z tematem stopień liczby.

Omówiono obliczanie logarytmu logarytm. Logarytm to matematyczna operacja polegająca na uzyskaniu logarytmu. Przy logarytmowaniu iloczyny czynników są przekształcane w sumy wyrazów.

Wzmocnienie jest operacją matematyczną odwrotną do logarytmu. Podczas wzmacniania dana podstawa jest podnoszona do potęgi wyrażenia, na którym przeprowadzane jest wzmacnianie. W tym przypadku sumy warunków są przekształcane w iloczyn czynników.

Dość często używa się logarytmów rzeczywistych o podstawach 2 (binarnie), e Liczba Eulera e ≈ 2,718 (logarytm naturalny) i 10 (dziesiętnie).

NA ten etap właściwe do rozważenia próbki logarytmów dziennik 7 2 , ln √ 5, lg0.0001.

A wpisy lg (-3), log -3 3,2, log -1 -4,3 nie mają sensu, ponieważ w pierwszym z nich liczba ujemna jest umieszczona pod znakiem logarytmu, w drugim - liczba ujemna w podstawie, aw trzeciej - i liczba ujemna pod znakiem logarytmu i jednostka w podstawie.

Warunki wyznaczania logarytmu.

Warto osobno rozważyć warunki a > 0, a ≠ 1, b > 0. Definicja logarytmu. Zastanówmy się, dlaczego wprowadzono te ograniczenia. Pomoże nam to z równością postaci x = log α B, zwaną podstawową tożsamością logarytmiczną, co bezpośrednio wynika z definicji logarytmu podanej powyżej.

Weź warunek a≠1. Ponieważ jeden jest równy jeden do dowolnej potęgi, to równość x=log α B może istnieć tylko wtedy, gdy b=1, ale log 1 1 będzie dowolną liczbą rzeczywistą. Aby wyeliminować tę niejednoznaczność, bierzemy a≠1.

Udowodnijmy konieczność warunku a>0. Na a=0 zgodnie ze sformułowaniem logarytmu, może istnieć tylko wtedy, gdy b=0. A potem odpowiednio dziennik 0 0 może być dowolną niezerową liczbą rzeczywistą, ponieważ zero do dowolnej niezerowej potęgi wynosi zero. Aby wyeliminować tę niejednoznaczność, warunek a≠0. I kiedy A<0 musielibyśmy odrzucić analizę racjonalnych i niewymiernych wartości logarytmu, ponieważ wykładnik z wykładnikiem wymiernym i niewymiernym jest zdefiniowany tylko dla nieujemnych podstaw. Z tego powodu warunek a>0.

I ostatni warunek b>0 wynika z nierówności a>0, ponieważ x=log α B, a wartość stopnia z dodatnią podstawą A zawsze pozytywny.

Cechy logarytmów.

Logarytmy charakteryzuje się charakterystycznym cechy, co doprowadziło do ich powszechnego stosowania w celu znacznego ułatwienia żmudnych obliczeń. W przejściu „do świata logarytmów” mnożenie zamienia się w dużo łatwiejsze dodawanie, dzielenie w odejmowanie, a podnoszenie do potęgi i pierwiastkowanie odpowiednio w mnożenie i dzielenie przez wykładnik.

Formuła logarytmów i tabela ich wartości (dla funkcji trygonometrycznych) została po raz pierwszy opublikowana w 1614 roku przez szkockiego matematyka Johna Napiera. Tablice logarytmiczne, powiększone i uszczegółowione przez innych naukowców, były szeroko stosowane w obliczeniach naukowych i inżynierskich i pozostały aktualne, dopóki nie zaczęto używać kalkulatorów elektronicznych i komputerów.

Definicja logarytmu

Logarytm liczby b do podstawy a to wykładnik, do którego należy podnieść a, aby uzyskać b.

liczba e w matematyce zwyczajowo określa się granicę, do której zmierza wyrażenie

numer e Jest Liczba niewymierna- liczba niewspółmierna z jedynką, nie można jej dokładnie wyrazić ani jako całość, ani jako ułamek racjonalny numer.

List mi- pierwsza litera słowa łacińskiego uniewinnić- afiszować się, stąd nazwa w matematyce wykładniczy- funkcja wykładnicza.

Numer mi szeroko stosowane w matematyce i we wszystkich naukach ścisłych, w taki czy inny sposób wykorzystujące obliczenia matematyczne do swoich potrzeb.

Logarytmy. Własności logarytmów

Definicja: Logarytm bazowy liczby dodatniej b to wykładnik c, do którego należy podnieść liczbę a, aby otrzymać liczbę b.

Podstawowa tożsamość logarytmiczna:

7) Formuła przejścia do nowej bazy:

lna = log e a, e ≈ 2,718…

Zadania i testy na temat „Logarytmy. Własności logarytmów»

• Logarytmy - Ważne tematy do powtarzania egzaminu z matematyki

Aby pomyślnie wykonać zadania z tego tematu, musisz znać definicję logarytmu, właściwości logarytmów, podstawową tożsamość logarytmiczną, definicje logarytmów dziesiętnych i naturalnych. Główne typy zadań na ten temat to zadania do obliczania i konwertowania wyrażeń logarytmicznych. Rozważmy ich rozwiązanie na poniższych przykładach.

Rozwiązanie: Korzystając z właściwości logarytmów, otrzymujemy

Rozwiązanie: korzystając z właściwości stopnia, otrzymujemy

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Własności logarytmów, formuły i dowody.

Logarytmy mają liczbę charakterystyczne właściwości. W tym artykule przeanalizujemy główne własności logarytmów. Tutaj podajemy ich sformułowania, zapisujemy właściwości logarytmów w postaci wzorów, pokazujemy przykłady ich zastosowania, a także podajemy dowody własności logarytmów.

Nawigacja po stronie.

Podstawowe własności logarytmów, wzory

Dla ułatwienia zapamiętania i użycia przedstawiamy podstawowe własności logarytmów jako lista formuł. W kolejnej części podajemy ich formułę, dowody, przykłady użycia i niezbędne wyjaśnienia.

Właściwość dziennika jednostek: log a 1=0 dla dowolnego a>0 , a≠1 .

logarytm liczby, równa podstawie: log a=1 dla a>0 , a≠1 .

Właściwość logarytmu stopnia podstawowego: log a a p = p , gdzie a>0 , a≠1 i p jest dowolną liczbą rzeczywistą.

Logarytm iloczynu dwóch liczb dodatnich: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
oraz właściwość logarytmu iloczynu n liczb dodatnich: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 > 0, …, xn > 0 .

Prywatna właściwość logarytmu: , gdzie a>0 , a≠1 , x>0 , y>0 .

Logarytm potęgi liczby: log a b p = p log a |b| , gdzie a>0 , a≠1 , b i p są liczbami takimi, że stopień b p ma sens i b p > 0 .

Konsekwencja: , gdzie a>0 , a≠1 , n – Liczba naturalna, większy niż jeden, b>0 .

Wniosek 1: , a>0 , a≠1 , b>0 , b≠1 .

Wniosek 2: , a>0 , a≠1 , b>0 , p i q są liczbami rzeczywistymi, q≠0 , w szczególności dla b=a mamy .

Twierdzenia i dowody właściwości

Przechodzimy do sformułowania i udowodnienia zarejestrowanych własności logarytmów. Wszystkie własności logarytmów są udowodnione na podstawie definicji logarytmu i podstawy tożsamość logarytmiczna, a także właściwości stopnia.

Zacznijmy własności logarytmu jedności. Jego sformułowanie jest następujące: logarytm jedności jest równy zero, to znaczy zaloguj 1=0 dla dowolnego a>0 , a≠1 . Dowód jest prosty: ponieważ a 0 = 1 dla każdego a, który spełnia powyższe warunki a>0 i a≠1 , to logarytm udowodnionej równości a 1 = 0 wynika bezpośrednio z definicji logarytmu.

Podajmy przykłady zastosowania rozważanej właściwości: log 3 1=0 , lg1=0 i .

Przejdźmy do następnej właściwości: logarytm liczby równej podstawie jest równy jeden, to jest, zaloguj a=1 dla a>0 , a≠1 . Rzeczywiście, ponieważ a 1 = a dla dowolnego a , to zgodnie z definicją logarytmu log a a = 1 .

Przykładami wykorzystania tej właściwości logarytmów są log 5 5=1 , log 5.6 5.6 i lne=1 .

Logarytm potęgi liczby równej podstawie logarytmu jest równy wykładnikowi. Ta właściwość logarytmu odpowiada formule postaci zaloguj a p = p, gdzie a>0 , a≠1 i p to dowolna liczba rzeczywista. Właściwość ta wynika bezpośrednio z definicji logarytmu. Zauważ, że pozwala to natychmiast określić wartość logarytmu, jeśli możliwe jest przedstawienie liczby pod znakiem logarytmu jako stopnia podstawy, porozmawiamy o tym więcej w artykule obliczanie logarytmów.

Na przykład log 2 2 7 =7 , log10 -4 =-4 i .

Logarytm iloczynu dwóch liczb dodatnich x i y jest równy produktowi logarytmy tych liczb: log a (x y)=log a x+log a y, a>0 , a≠1 . Udowodnijmy własność logarytmu produktu. Ze względu na własności stopnia a log a x + log a y =a log a x a log a y , a ponieważ z głównej tożsamości logarytmicznej a log a x = x i log a y = y , to log a x a log a y = x y . Zatem log a x+log a y = x y , skąd wymagana równość wynika z definicji logarytmu.

Pokażmy przykłady wykorzystania własności logarytmu iloczynu: log 5 (2 3)=log 5 2+log 5 3 oraz .

Właściwość logarytmu iloczynu można uogólnić na iloczyn skończonej liczby n liczb dodatnich x 1 , x 2 , …, x n jako log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Tę równość można łatwo udowodnić metodą indukcji matematycznej.

Na przykład logarytm naturalny iloczynu można zastąpić sumą trzech logarytmów naturalnych liczb 4 , e i .

Logarytm ilorazu dwóch liczb dodatnich x i y są równe różnicy między logarytmami tych liczb. Właściwość ilorazu logarytmu odpowiada formule postaci , gdzie a>0 , a≠1 , x i y to pewne liczby dodatnie. Ważność tego wzoru jest udowodniona podobnie jak wzór na logarytm iloczynu: ponieważ , to przez definicję logarytmu .

Oto przykład użycia tej właściwości logarytmu: .

Przejdźmy do własność logarytmu stopnia. Logarytm stopnia jest równy iloczynowi wykładnika i logarytmu modułu podstawy tego stopnia. Piszemy tę właściwość logarytmu stopnia w postaci wzoru: log a b p =p log a |b|, gdzie a>0 , a≠1 , b i p są liczbami takimi, że stopień b p ma sens i b p > 0 .

Najpierw udowodnimy tę własność dla pozytywnego b . Podstawowa tożsamość logarytmiczna pozwala nam przedstawić liczbę b jako log a b , wtedy b p = (a log a b) p , a wynikowe wyrażenie, ze względu na właściwość potęgi, jest równe a p log a b . Dochodzimy więc do równości b p = a p log a b , z której na podstawie definicji logarytmu wnioskujemy, że log a b p = p log a b .

Pozostaje udowodnić tę własność dla ujemnego b . Zauważmy tutaj, że wyrażenie log a b p dla ujemnego b ma sens tylko dla parzystych wykładników p (ponieważ wartość stopnia b p musi być większa od zera, inaczej logarytm nie będzie miał sensu), iw tym przypadku b p =|b| P . Wtedy bp =|b| p =(a log a |b|) p =a p log a |b| , skąd log a b p =p log a |b| .

Na przykład, oraz ln(-3) 4 =4 ln|-3|=4 ln3 .

Wynika to z poprzedniej własności właściwość logarytmu od pierwiastka: logarytm pierwiastka n-tego stopnia jest równy iloczynowi ułamka 1/n i logarytmu pierwiastka wyrażenia, czyli gdzie a>0, a≠1, n jest liczbą naturalną większą od jeden, b>0.

Dowód opiera się na równości (patrz definicja wykładnika z wykładnikiem ułamkowym), która obowiązuje dla dowolnego dodatniego b oraz własności logarytmu stopnia: .

Oto przykład użycia tej właściwości: .

Teraz udowodnijmy formułę konwersji na nową podstawę logarytmu Uprzejmy . Aby to zrobić, wystarczy udowodnić poprawność równości log c b=log a b log c a . Podstawowa tożsamość logarytmiczna pozwala nam przedstawić liczbę b jako log a b , a następnie log c b = log c a log a b . Pozostaje skorzystać z własności logarytmu stopnia: log c a log a b = log a b log c a . W ten sposób udowodniono równość log c b=log a b log c a, co oznacza, że ​​udowodniono również wzór na przejście do nowej podstawy logarytmu .

Pokażmy kilka przykładów zastosowania tej właściwości logarytmów: i .

Formuła przejścia do nowej podstawy pozwala przejść do pracy z logarytmami, które mają „wygodną” podstawę. Na przykład można go użyć do przełączenia na logarytmy naturalne lub dziesiętne, aby można było obliczyć wartość logarytmu z tabeli logarytmów. Formuła przejścia do nowej podstawy logarytmu pozwala również w niektórych przypadkach znaleźć wartość danego logarytmu, gdy znane są wartości niektórych logarytmów o innych podstawach.

Używany często szczególny przypadek wzory na przejście do nowej podstawy logarytmu dla c=b postaci . To pokazuje, że log a b i log b a są liczbami wzajemnie odwrotnymi. Np, .

Formuła jest również często używana, co jest wygodne przy znajdowaniu wartości logarytmicznych. Na potwierdzenie naszych słów pokażemy, jak obliczana jest za jego pomocą wartość logarytmu formularza. Mamy . Aby udowodnić wzór, wystarczy użyć wzoru przejścia do nowej podstawy logarytmu a: .

Pozostaje udowodnić właściwości porównawcze logarytmów.

Użyjmy odwrotnej metody. Załóżmy, że dla a 1 >1 , a 2 >1 i a 1 2 oraz dla 0 1 log a 1 b≤ log a 2 b jest prawdziwe. Dzięki właściwościom logarytmów nierówności te można zapisać jako I odpowiednio, az nich wynika, że ​​odpowiednio log b a 1 ≤ log b a 2 i log b a 1 ≥log b a 2. Następnie przez właściwości potęg z te same podstawy równości b log b a 1 ≥b log b a 2 i b log b a 1 ≥b log b a 2 muszą być spełnione, czyli a 1 ≥a 2 . W ten sposób doszliśmy do sprzeczności z warunkiem a 1 2 . To kończy dowód.

Podstawowe własności logarytmów

• Materiały do ​​lekcji
• Pobierz wszystkie formuły

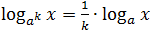
Logarytmy, jak każdą liczbę, można dodawać, odejmować i konwertować na wszelkie możliwe sposoby. Ale ponieważ logarytmy nie są całkiem zwykłymi liczbami, istnieją tutaj reguły, które są nazywane podstawowe właściwości.

Te zasady muszą być znane - bez nich nie da się rozwiązać żadnego poważnego problemu logarytmicznego. Ponadto jest ich bardzo mało - wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.

Dodawanie i odejmowanie logarytmów

Rozważmy dwa logarytmy o tej samej podstawie: log a x i log a y . Następnie można je dodawać i odejmować oraz:

Zatem suma logarytmów jest równa logarytmowi iloczynu, a różnica jest logarytmem ilorazu. Notatka: kluczowy moment Tutaj - te same podstawy. Jeśli podstawy są różne, te zasady nie działają!

Formuły te pomogą obliczyć wyrażenie logarytmiczne, nawet jeśli jego poszczególne części nie są brane pod uwagę (patrz lekcja „Co to jest logarytm”). Spójrz na przykłady - i zobacz:

Zadanie. Znajdź wartość wyrażenia: log 6 4 + log 6 9.

Ponieważ podstawy logarytmów są takie same, używamy wzoru na sumę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadanie. Znajdź wartość wyrażenia: log 2 48 − log 2 3.

Podstawy są takie same, używamy wzoru na różnicę:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadanie. Znajdź wartość wyrażenia: log 3 135 − log 3 5.

Ponownie, podstawy są takie same, więc mamy:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Jak widać, oryginalne wyrażenia składają się z „złych” logarytmów, które nie są rozpatrywane osobno. Ale po przekształceniach okazuje się całkiem normalne numery. Opierając się na tym fakcie, wielu papiery testowe. Tak, ta kontrola - podobne wyrażenia z całą powagą (czasami - praktycznie bez zmian) są oferowane na egzaminie.

Usuwanie wykładnika z logarytmu

Teraz skomplikujmy trochę zadanie. Co jeśli w podstawie lub argumencie logarytmu jest stopień? Następnie wykładnik tego stopnia można wyjąć ze znaku logarytmu zgodnie z następującymi zasadami:

• log a x n = n log a x ;
• 
• 

Łatwo to zauważyć ostatnia zasada podąża za dwoma pierwszymi. Ale i tak lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.

Oczywiście wszystkie te zasady mają sens, jeśli obserwuje się logarytm ODZ: a > 0, a ≠ 1, x > 0. I jeszcze jedno: naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale także odwrotnie, tj. możesz wprowadzić liczby przed znakiem logarytmu do samego logarytmu. To jest najczęściej wymagane.

Zadanie. Znajdź wartość wyrażenia: log 7 49 6 .

Pozbądźmy się stopnia w argumencie według pierwszego wzoru:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadanie. Znajdź wartość wyrażenia:

[Podpis ilustracji]

Zauważ, że mianownik jest logarytmem, którego podstawą i argumentem są potęgi dokładne: 16 = 2 4 ; 49 = 72. Mamy:

[Podpis ilustracji]

Myślę, że ostatni przykład wymaga wyjaśnienia. Gdzie się podziały logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawili podstawę i argument stojącego tam logarytmu w postaci stopni i wyjęli wskaźniki - otrzymali ułamek „trzypiętrowy”.

Teraz spójrzmy na ułamek główny. Licznik i mianownik mają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0, możemy skrócić ułamek - 2/4 pozostanie w mianowniku. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co zostało zrobione. Wynikiem jest odpowiedź: 2.

Przejście na nowy fundament

Mówiąc o zasadach dodawania i odejmowania logarytmów, wyraźnie podkreśliłem, że działają one tylko z tymi samymi podstawami. A co jeśli podstawy są inne? Co jeśli nie są to dokładne potęgi tej samej liczby?

Na ratunek przychodzą formuły przejścia do nowej bazy. Formułujemy je w postaci twierdzenia:

Niech logarytm logarytmiczny a x będzie dany. Wtedy dla dowolnej liczby c takiej, że c > 0 i c ≠ 1, równość jest prawdziwa:

[Podpis ilustracji]

W szczególności, jeśli wstawimy c = x , otrzymamy:

[Podpis ilustracji]

Z drugiej formuły wynika, że ​​można zamienić podstawę i argument logarytmu, ale w tym przypadku całe wyrażenie jest „odwrócone”, tj. logarytm jest w mianowniku.

Formuły te rzadko występują w zwykłych wyrażeniach liczbowych. Można ocenić, jak wygodne są tylko przy podejmowaniu decyzji równania logarytmiczne i nierówności.

Są jednak zadania, których w ogóle nie można rozwiązać, chyba że przeprowadzi się do nowego fundamentu. Rozważmy kilka z nich:

Zadanie. Znajdź wartość wyrażenia: log 5 16 log 2 25.

Zauważ, że argumenty obu logarytmów są dokładnymi wykładnikami. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Teraz odwróćmy drugi logarytm:

[Podpis ilustracji]

Ponieważ iloczyn nie zmienia się z permutacji czynników, spokojnie pomnożyliśmy cztery i dwa, a następnie obliczyliśmy logarytmy.

Zadanie. Znajdź wartość wyrażenia: log 9 100 lg 3.

Podstawą i argumentem pierwszego logarytmu są potęgi dokładne. Zapiszmy to i pozbądźmy się wskaźników:

[Podpis ilustracji]

Teraz pozbądźmy się logarytmu dziesiętnego, przechodząc do nowej podstawy:

[Podpis ilustracji]

Podstawowa tożsamość logarytmiczna

Często w procesie rozwiązywania wymagane jest przedstawienie liczby jako logarytmu do danej podstawy. W takim przypadku formuły pomogą nam:

1. n = log a a n

2. W pierwszym przypadku liczba n staje się wykładnikiem w argumencie. Liczba n może być absolutnie dowolna, ponieważ jest to po prostu wartość logarytmu.

   Druga formuła jest w rzeczywistości sparafrazowaną definicją. Nazywa się to podstawową tożsamością logarytmiczną.

   Rzeczywiście, co się stanie, jeśli liczbę b podniesiemy do takiej potęgi, że liczba b do tej potęgi da liczbę a? Zgadza się: to jest ta sama liczba a . Przeczytaj uważnie ten akapit jeszcze raz - wiele osób się na nim "wiesza".

   Podobnie jak nowe formuły konwersji bazowej, podstawowa tożsamość logarytmiczna jest czasem jedynym możliwym rozwiązaniem.

   [Podpis ilustracji]

   Zauważ, że log 25 64 = log 5 8 - po prostu weź kwadrat podstawy i argument logarytmu. Biorąc pod uwagę zasady mnożenia potęg o tej samej podstawie, otrzymujemy:

   [Podpis ilustracji]

   Jeśli ktoś nie wie, to było prawdziwe zadanie z Jednolitego Egzaminu Państwowego 🙂

   Jednostka logarytmiczna i zero logarytmiczne

   Na zakończenie podam dwie tożsamości, które trudno nazwać własnościami – są to raczej konsekwencje z definicji logarytmu. Ciągle znajdują się w problemach i, co zaskakujące, stwarzają problemy nawet dla „zaawansowanych” uczniów.

   1. log a a = 1 to jednostka logarytmiczna. Zapamiętaj raz na zawsze: logarytm do dowolnej podstawy a z samej tej podstawy jest równy jeden.
   2. log a 1 = 0 to zero logarytmiczne. Podstawa a może być dowolna, ale jeśli argumentem jest jeden - logarytm wynosi zero! Ponieważ 0 = 1 jest bezpośrednią konsekwencją definicji.

   To wszystkie właściwości. Pamiętaj, aby ćwiczyć wprowadzanie ich w życie! Pobierz ściągawkę na początku lekcji, wydrukuj ją - i rozwiąż zadania.

   Logarytm. Własności logarytmu (dodawanie i odejmowanie).

   Własności logarytmu wynikać z jego definicji. I tak logarytm liczby B z powodu A zdefiniowany jako wykładnik, do którego należy podnieść liczbę A aby uzyskać numer B(logarytm istnieje tylko dla liczb dodatnich).

   Z tego sformułowania wynika, że ​​obliczenie x=log a b, jest równoważne rozwiązaniu równania topór=b. Na przykład, log 2 8 = 3 ponieważ 8 = 2 3 . Sformułowanie logarytmu pozwala uzasadnić, że jeśli b=a do, a następnie logarytm liczby B z powodu A równa się Z. Oczywiste jest również, że temat logarytmu jest ściśle powiązany z tematem potęgi liczby.

   Z logarytmami, jak z dowolnymi liczbami, możesz wykonać operacje dodawania, odejmowania i przekształcać w każdy możliwy sposób. Ale ze względu na fakt, że logarytmy nie są całkiem zwykłymi liczbami, obowiązują tutaj ich własne specjalne zasady, zwane podstawowe właściwości.

   Dodawanie i odejmowanie logarytmów.

   Weź dwa logarytmy o tej samej podstawie: dziennik x I zaloguj się. Następnie usuń możliwe jest wykonywanie operacji dodawania i odejmowania:

   jak widzimy, suma logarytmów jest równy logarytmowi iloczynu, oraz różnica logarytmy- logarytm ilorazu. I to prawda, jeśli liczby A, X I Na pozytywne i a ≠ 1.

   Należy zauważyć, że głównym aspektem tych formuł są te same zasady. Jeśli podstawy różnią się od siebie, te zasady nie mają zastosowania!

   Zasady dodawania i odejmowania logarytmów o tych samych podstawach są odczytywane nie tylko od lewej do prawej, ale także odwrotnie. W rezultacie mamy twierdzenia dotyczące logarytmu iloczynu i logarytmu ilorazu.

   Logarytm produktu dwie liczby dodatnie są równe sumie ich logarytmów ; parafrazując to twierdzenie, otrzymujemy, jeśli liczby A, X I Na pozytywne i a ≠ 1, To:

   Logarytm ilorazu dwóch liczb dodatnich jest równa różnicy między logarytmami dzielnej i dzielnej. Innymi słowy, jeśli liczby A, X I Na pozytywne i a ≠ 1, To:

   Powyższe twierdzenia stosujemy do rozwiązania przykłady:

   Jeśli liczby X I Na są wtedy ujemne formuła logarytmu iloczynu staje się bez sensu. Zabrania się więc pisania:

   ponieważ wyrażenia log 2 (-8) i log 2 (-4) nie są w ogóle zdefiniowane (funkcja logarytmiczna Na= dziennik 2 X zdefiniowane tylko dla dodatnich wartości argumentu X).

   Twierdzenie o produkcie ma zastosowanie nie tylko do dwóch, ale także do nieograniczonej liczby czynników. Oznacza to, że dla każdego naturalnego k i dowolne liczby dodatnie X 1 , X 2 , . . . ,x rz istnieje tożsamość:

   Z Twierdzenia o logarytmach ilorazowych można uzyskać jeszcze jedną właściwość logarytmu. Ten dziennik jest dobrze znany A 1= 0, zatem

   Istnieje więc równość:

   Logarytmy dwóch wzajemnie odwrotnych liczb na tej samej podstawie będą się różnić od siebie tylko znakiem. Więc:

   Logarytm. Własności logarytmów

   Logarytm. Własności logarytmów

   Rozważ równość. Daj nam znać wartości i chcemy znaleźć wartość .

   Oznacza to, że szukamy wykładnika, do którego trzeba się nagiąć, aby uzyskać .

   Pozwalać zmienna może przyjąć dowolną wartość rzeczywistą, wówczas na zmienne nakładane są następujące ograniczenia: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Jeśli znamy wartości i , a przed nami zadanie znalezienia nieznanego, to w tym celu wprowadzana jest operacja matematyczna, która nazywa się logarytm.

   Aby znaleźć wartość, którą bierzemy logarytm liczby Przez Fundacja :

   Logarytm liczby do podstawy to wykładnik, do którego należy podnieść, aby uzyskać .

   To jest podstawowa tożsamość logarytmiczna:

   o” tytuł=”a>o”/> , 1″ tytuł=”a1″/>, 0″ tytuł=”b>0″/>

   jest zasadniczo zapisem matematycznym definicje logarytmów.

   Logarytm operacji matematycznej jest odwrotnością potęgowania, więc własności logarytmów są ściśle związane z właściwościami stopnia.

   Wymieniamy główne własności logarytmów:

   (o” tytuł=”a>o”/> , 1″ tytuł=”a1″/>, 0″ tytuł=”b>0″/>, 0,

   d>0″/>, 1″ tytuł=”d1″/>

   4.

   5.

   Poniższa grupa właściwości pozwala przedstawić wykładnik wyrażenia pod znakiem logarytmu lub stojący u podstawy logarytmu jako współczynnik przed znakiem logarytmu:

   6.

   7.

   8.

   9.

   Kolejna grupa wzorów pozwala przejść od logarytmu o podanej podstawie do logarytmu o dowolnej podstawie i nazywa się formuły przejścia do nowej bazy:

   10.

   12. (wynik z właściwości 11)

   

   Następujące trzy właściwości nie są dobrze znane, ale są często używane podczas rozwiązywania równań logarytmicznych lub podczas upraszczania wyrażeń zawierających logarytmy:

   13.

   14.

   15.

   Przypadki specjalne:

   — logarytm dziesiętny

   — naturalny logarytm

   Podczas upraszczania wyrażeń zawierających logarytmy stosuje się ogólne podejście:

   1. Wprowadzenie dziesiętne w postaci zwykłego.

   2. liczby mieszane reprezentowane jako ułamki niewłaściwe.

   3. Liczby u podstawy logarytmu i pod znakiem logarytmu rozkłada się na czynniki pierwsze.

   4. Staramy się sprowadzić wszystkie logarytmy do tej samej podstawy.

   5. Zastosuj własności logarytmów.

   Przyjrzyjmy się przykładom upraszczania wyrażeń zawierających logarytmy.

   Przykład 1

   Oblicz:

   Uprośćmy wszystkie wykładniki: naszym zadaniem jest doprowadzić je do logarytmów, których podstawa jest taka sama jak podstawa wykładnika.

   ==(według właściwości 7)=(według właściwości 6) =

   Zastąp wskaźniki, które uzyskaliśmy w oryginalnym wyrażeniu. Otrzymujemy:

   Odpowiedź: 5.25

   Przykład 2 Oblicz:

   

   Doprowadzamy wszystkie logarytmy do podstawy 6 (w tym przypadku logarytmy z mianownika ułamka „migrują” do licznika):

   Rozłóżmy liczby pod znakiem logarytmu na czynniki pierwsze:

   Zastosuj właściwości 4 i 6:

   Przedstawiamy zamiennik

   Otrzymujemy:

   Odpowiedź 1

   Logarytm . Podstawowa tożsamość logarytmiczna.

   Własności logarytmów. Logarytm dziesiętny. naturalny logarytm.

   logarytm liczba dodatnia N w bazie (B > 0, B 1) nazywa się wykładnikiem x, do którego należy podnieść b, aby otrzymać N .

   Ten wpis jest równoważny następującemu: b x = N .

   PRZYKŁADY: log 3 81 = 4 ponieważ 3 4 = 81 ;

   log 1/3 27 = – 3 ponieważ (1/3) - 3 = 3 3 = 27 .

   Powyższą definicję logarytmu można zapisać jako tożsamość:

   

   Podstawowe własności logarytmów.

   2) log 1 = 0, ponieważ B 0 = 1 .

   3) Logarytm iloczynu jest równy sumie logarytmów czynników:

   4) Logarytm ilorazu jest równy różnicy między logarytmami dzielnej i dzielnikiem:

   5) Logarytm stopnia jest równy iloczynowi wykładnika i logarytmu jego podstawy:

   Konsekwencja tej właściwości jest następująca: katalog główny jest równy logarytmowi liczba pierwiastków podzielona przez stopień pierwiastka:

   

   6) Jeśli podstawą logarytmu jest potęga, to wartość odwrotność wykładnika można wyjąć ze znaku dziennika rymów:

   

   Dwie ostatnie właściwości można połączyć w jedną:

   

   7) Wzór na moduł przejściowy (tj. przejście od jednej podstawy logarytmu do drugiej podstawy):

   

   W konkretnym przypadku, kiedy N = za mamy:

   

   Logarytm dziesiętny zwany logarytm bazowy 10. Oznacza się lg, tj. dziennik 10 N= dziennik N. Logarytmy liczb 10, 100, 1000, . p to odpowiednio 1, 2, 3, …, tj. mieć tyle pozytywów

   jednostki, ile zer jest w liczbie logarytmicznej po jedynki. Logarytmy liczb 0,1, 0,01, 0,001, . p to odpowiednio –1, –2, –3, …, tj. mieć tyle jedynek ujemnych, ile jest zer w logarytmie przed jedynką (wliczając zera). Logarytmy pozostałych liczb mają część ułamkową tzw mantysa. Nazywa się część całkowitą logarytmu Charakterystyka. W zastosowaniach praktycznych najwygodniejsze są logarytmy dziesiętne.

   naturalny logarytm zwany logarytm bazowy mi. Jest oznaczony przez ln, tj. dziennik mi N= ln N. Numer mi jest irracjonalny, jego przybliżona wartość to 2,718281828. Jest to granica, do której zbliża się liczba (1 + 1 / N) N z nieograniczonym wzrostem N(cm. Pierwszy cudowna granica na stronie „Ograniczenia”. ciągi liczb»).
   Choć może się to wydawać dziwne, logarytmy naturalne okazały się bardzo wygodne przy przeprowadzaniu różnych operacji związanych z analizą funkcji. Obliczanie logarytmów bazowych mi znacznie szybciej niż jakakolwiek inna baza.

• Czego potrzebujesz dzisiaj, aby adoptować dziecko w Rosji? Adopcja w Rosji, oprócz odpowiedzialnej decyzji personalnej, wiąże się z szeregiem procedur państwowej weryfikacji kandydatów. Trudny wybór dla etap przygotowawczy przyczynia się do większej […]
• Informacje o NIP lub OGRN za darmo z rejestru podatkowego w całej Rosji - online Na ujednoliconym portalu usług podatkowych można uzyskać informacje o rejestracji państwowej osoby prawne, indywidualni przedsiębiorcy, […]
• Kara za jazdę bez dokumentów (prawo jazdy, ubezpieczenie, STS) Czasami z powodu zapomnienia kierowcy wsiadają za kierownicę bez prawa jazdy i otrzymują mandat za jazdę bez dokumentów. Przypomnijmy, że jadący z nim kierowca bezbłędnie […]
• Kwiaty dla mężczyzn. Jakie kwiaty można podarować mężczyźnie? Jakie kwiaty można podarować mężczyźnie? Nie ma tak wielu „męskich” kwiatów, ale są takie, które są dane mężczyznom. Mała lista kwiatów przed tobą: Chryzantemy. róże. Goździki. […]
• notatka jest specjalną formą dokumentu używaną w środowisko wewnętrzne przedsiębiorstwa i służy szybkiemu rozwiązywaniu bieżących problemów produkcyjnych. Zwykle dokument ten jest sporządzany w celu dokonania pewnych […]
• Kiedy i jak uzyskać finansowaną część emerytury w Sbierbanku? Sberbank jest bankiem partnerskim państwowego funduszu emerytalnego. Na tej podstawie obywatele, którzy wyemitowali kapitałową emeryturę, mogli przenieść kapitałową […]
• Zasiłki na dzieci w Uljanowsku i obwodzie uljanowskim w 2018 r. Ponadto we wszystkich regionach działają programy zatwierdzone przez prawo federalne. Zobaczmy, na kogo i na jakie świadczenia mogą liczyć. Jak władze regionalne […]
• Szczegółowy poradnik jak sporządzić pełnomocnictwo do reprezentowania interesów indywidualny w sądzie W pozwie cywilnym lub arbitrażowym, w sprawie administracyjnej lub karnej interesy zarówno powoda, jak i pozwanego mogą być reprezentowane przez pełnomocnika: […]

Instrukcja

Zapisz podane wyrażenie logarytmiczne. Jeśli wyrażenie używa logarytmu 10, to jego zapis jest skracany i wygląda następująco: lg b jest logarytmem dziesiętnym. Jeżeli podstawą logarytmu jest liczba e, to zapisuje się wyrażenie: ln b jest logarytmem naturalnym. Rozumie się, że wynikiem any jest potęga, do której należy podnieść liczbę podstawową, aby uzyskać liczbę b.

Gdy znajdujesz sumę dwóch funkcji, wystarczy rozróżnić je jedna po drugiej i dodać wyniki: (u+v)" = u"+v";

Aby znaleźć pochodną iloczynu dwóch funkcji, należy pomnożyć pochodną pierwszej funkcji przez drugą i dodać pochodną drugiej funkcji pomnożoną przez pierwszą funkcję: (u*v)" = u"* v+v"*u;

Aby znaleźć pochodną ilorazu dwóch funkcji, należy od iloczynu pochodnej dywidendy pomnożonej przez funkcję dzielnika odjąć iloczyn pochodnej dzielnika pomnożonej przez funkcję dzielnika i podzielić wszystko to przez funkcję dzielnika do kwadratu. (u/v)" = (u"*v-v"*u)/v^2;

Jeśli podano złożona funkcja, to trzeba pomnożyć pochodną funkcja wewnętrzna i pochodną zewnętrznej. Niech y=u(v(x)), wtedy y"(x)=y"(u)*v"(x).

Korzystając z powyższego, możesz rozróżnić prawie każdą funkcję. Spójrzmy więc na kilka przykładów:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *X));
Są też zadania do obliczania pochodnej w punkcie. Niech funkcja y=e^(x^2+6x+5) będzie dana, musisz znaleźć wartość funkcji w punkcie x=1.
1) Znajdź pochodną funkcji: y"=e^(x^2-6x+5)*(2*x +6).

2) Oblicz wartość funkcji w dany punkt y"(1)=8*e^0=8

Powiązane wideo

Pomocna rada

Naucz się tabeli pochodnych elementarnych. Pozwoli to zaoszczędzić dużo czasu.

Źródła:

• stała pochodna

Więc jaka jest różnica między racjonalne równanie od racjonalnego? Jeśli nieznana zmienna znajduje się pod znakiem pierwiastek kwadratowy, to równanie jest uważane za niewymierne.

Instrukcja

Główną metodą rozwiązywania takich równań jest metoda podnoszenia obu stron równania w kwadrat. Jednakże. jest to naturalne, pierwszym krokiem jest pozbycie się znaku. Technicznie ta metoda nie jest trudna, ale czasami może prowadzić do kłopotów. Na przykład równanie v(2x-5)=v(4x-7). Podnosząc obie strony do kwadratu, otrzymujesz 2x-5=4x-7. Takie równanie nie jest trudne do rozwiązania; x=1. Ale numer 1 nie zostanie nadany równania. Dlaczego? Zastąp jednostkę w równaniu zamiast wartości x. A prawa i lewa strona będą zawierać wyrażenia, które nie mają sensu, to znaczy. Taka wartość nie jest poprawna dla pierwiastka kwadratowego. Dlatego 1 jest zewnętrznym pierwiastkiem, a zatem to równanie nie ma pierwiastków.

Tak więc irracjonalne równanie rozwiązuje się metodą podniesienia do kwadratu obu jego części. Po rozwiązaniu równania konieczne jest odcięcie obcych korzeni. Aby to zrobić, zastąp znalezione pierwiastki oryginalnym równaniem.

Rozważ inny.
2x+vx-3=0
Oczywiście to równanie można rozwiązać za pomocą tego samego równania, co poprzednie. Związki transferowe równania, które nie mają pierwiastka kwadratowego, prawa strona a następnie zastosować metodę kwadratową. rozwiązać wynikowe równanie wymierne i pierwiastki. Ale inny, bardziej elegancki. Wprowadź nową zmienną; vx=y. W związku z tym otrzymasz równanie takie jak 2y2+y-3=0. Czyli zwykły równanie kwadratowe. Znajdź jego korzenie; y1=1 i y2=-3/2. Następnie rozwiąż dwa równania vx=1; vx \u003d -3/2. Drugie równanie nie ma pierwiastków, z pierwszego wynika, że ​​x=1. Nie zapomnij o konieczności sprawdzenia korzeni.

Rozwiązywanie tożsamości jest dość łatwe. To wymaga zrobienia identyczne przekształcenia aż do osiągnięcia celu. W ten sposób zadanie zostanie rozwiązane za pomocą najprostszych operacji arytmetycznych.

Będziesz potrzebować

• - papier;
• - długopis.

Instrukcja

Najprostsze takie przekształcenia to algebraiczne skrócone mnożenia (takie jak kwadrat sumy (różnica), różnica kwadratów, suma (różnica), sześcian sumy (różnica)). Ponadto istnieje wiele wzorów trygonometrycznych, które są zasadniczo tymi samymi tożsamościami.

Rzeczywiście, kwadrat sumy dwóch wyrazów jest równy kwadratowi pierwszego plus dwukrotność iloczynu pierwszego i drugiego plus kwadrat drugiego, czyli (a+b)^2= (a+b )(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Uprość oba

Ogólne zasady rozwiązania

Powtórz z podręcznika analizy matematycznej lub matematyki wyższej, która jest całką oznaczoną. Jak wiesz, rozwiązanie określona całka istnieje funkcja, której pochodna da całkę. Ta funkcja nazywa się prymitywnym. Zgodnie z tą zasadą konstruowane są całki podstawowe.
Określ na podstawie postaci całki, która z całek tabeli jest odpowiednia w tym przypadku. Nie zawsze da się to ustalić od razu. Często forma tabelaryczna staje się zauważalna dopiero po kilku przekształceniach w celu uproszczenia całki.

Metoda podstawienia zmiennej

Jeśli całka jest funkcją trygonometryczną, której argumentem jest jakiś wielomian, to spróbuj użyć metody zamiany zmiennych. Aby to zrobić, zastąp wielomian w argumencie całki jakąś nową zmienną. Na podstawie stosunku między nową a starą zmienną wyznacz nowe granice całkowania. Różniczkując to wyrażenie, znajdź nową różnicę w . W ten sposób otrzymasz nowy rodzaj poprzednia całka, bliska lub nawet odpowiadająca dowolnej tabelarycznej.

Rozwiązywanie całek drugiego rodzaju

Jeśli całka jest całką drugiego rodzaju, postacią wektorową całki, wówczas będziesz musiał zastosować reguły przejścia od tych całek do całek skalarnych. Jedną z takich reguł jest stosunek Ostrogradskiego-Gaussa. Prawo to umożliwia przejście od przepływu wirnika jakiejś funkcji wektorowej do potrójnej całki po rozbieżności danego pola wektorowego.

Podstawianie granic całkowania

Po znalezieniu funkcji pierwotnej konieczne jest podstawienie granic całkowania. Najpierw wstaw wartość górnej granicy do wyrażenia funkcji pierwotnej. Otrzymasz jakiś numer. Następnie odejmij od wynikowej liczby inną liczbę, wynikową dolną granicę funkcji pierwotnej. Jeśli jedną z granic integracji jest nieskończoność, to podstawiając ją do funkcja pierwotna konieczne jest dojście do granicy i znalezienie tego, do czego zmierza wyrażenie.
Jeśli całka jest dwuwymiarowa lub trójwymiarowa, będziesz musiał przedstawić geometryczne granice całkowania, aby zrozumieć, jak obliczyć całkę. Rzeczywiście, w przypadku, powiedzmy, całki trójwymiarowej, granicami całkowania mogą być całe płaszczyzny, które ograniczają całkowaną objętość.

Kontynuujemy naukę logarytmów. W tym artykule porozmawiamy o obliczanie logarytmów, proces ten nazywa się logarytm. Najpierw zajmiemy się obliczaniem logarytmów z definicji. Następnie zastanów się, w jaki sposób wartości logarytmów są znajdowane za pomocą ich właściwości. Następnie zajmiemy się obliczaniem logarytmów na podstawie początkowo podanych wartości innych logarytmów. Na koniec nauczmy się korzystać z tablic logarytmów. Cała teoria jest opatrzona przykładami ze szczegółowymi rozwiązaniami.

Nawigacja po stronie.

Obliczanie logarytmów z definicji

W najprostszych przypadkach możliwe jest szybkie i łatwe wykonanie znalezienie logarytmu z definicji. Przyjrzyjmy się bliżej, jak przebiega ten proces.

Jej istotą jest przedstawienie liczby b w postaci a c , skąd z definicji logarytmu liczba c jest wartością logarytmu. Oznacza to, że z definicji znalezienie logarytmu odpowiada następującemu łańcuchowi równości: log a b=log a a c =c .

Tak więc obliczenie logarytmu z definicji sprowadza się do znalezienia takiej liczby c, że a c \u003d b, a sama liczba c jest pożądaną wartością logarytmu.

Biorąc pod uwagę informacje z poprzednich akapitów, gdy liczba pod znakiem logarytmu jest podawana przez pewien stopień podstawy logarytmu, można od razu wskazać, czemu równy jest logarytm - jest równy wykładnikowi. Pokażmy przykłady.

Przykład.

Znajdź log 2 2 −3 , a także oblicz logarytm naturalny z e 5,3 .

Rozwiązanie.

Definicja logarytmu pozwala od razu powiedzieć, że log 2 2 −3 = −3 . Rzeczywiście, liczba pod znakiem logarytmu jest równa podstawie 2 do potęgi −3.

Podobnie znajdujemy drugi logarytm: lne 5,3 = 5,3.

Odpowiedź:

log 2 2 −3 = −3 i lne 5,3 = 5,3 .

Jeśli liczba b pod znakiem logarytmu nie jest podana jako potęga podstawy logarytmu, należy dokładnie rozważyć, czy możliwe jest przedstawienie reprezentacji liczby b w postaci a c . Często ta reprezentacja jest dość oczywista, zwłaszcza gdy liczba pod znakiem logarytmu jest równa podstawie do potęgi 1, lub 2, lub 3, ...

Przykład.

Oblicz logarytmy log 5 25 , i .

Rozwiązanie.

Łatwo zauważyć, że 25=5 2 , to pozwala obliczyć pierwszy logarytm: log 5 25=log 5 5 2 =2 .

Przechodzimy do obliczenia drugiego logarytmu. Liczbę można przedstawić jako potęgę liczby 7: (zobacz w razie potrzeby). Stąd, .

Przepiszmy trzeci logarytm w następującej postaci. Teraz możesz to zobaczyć , skąd to wnioskujemy . Dlatego z definicji logarytmu .

W skrócie rozwiązanie można zapisać w następujący sposób:

Odpowiedź:

dziennik 5 25=2 , I .

Gdy wystarczająco duża liczba naturalna znajduje się pod znakiem logarytmu, nie zaszkodzi rozłożyć ją na czynniki pierwsze. Często pomaga przedstawienie takiej liczby jako pewnej potęgi podstawy logarytmu, a zatem obliczenie tego logarytmu z definicji.

Przykład.

Znajdź wartość logarytmu.

Rozwiązanie.

Niektóre właściwości logarytmów umożliwiają natychmiastowe określenie wartości logarytmów. Właściwości te obejmują własność logarytmu jedynki i logarytmu liczby równej podstawie: log 1 1=log a a 0 =0 i log a a=log a a 1 =1 . Oznacza to, że gdy liczba 1 lub liczba a znajduje się pod znakiem logarytmu, równym podstawie logarytmu, wówczas w tych przypadkach logarytmy wynoszą odpowiednio 0 i 1.

Przykład.

Co to są logarytmy i lg10?

Rozwiązanie.

Ponieważ , wynika to z definicji logarytmu .

W drugim przykładzie liczba 10 pod znakiem logarytmu pokrywa się z jego podstawą, więc logarytm dziesiętny z dziesięciu jest równy jeden, czyli lg10=lg10 1 =1 .

Odpowiedź:

I lg10=1 .

Zauważ, że obliczanie logarytmów z definicji (co omówiliśmy w poprzednim akapicie) implikuje użycie logarytmu równości a a p = p , który jest jedną z właściwości logarytmów.

W praktyce, gdy liczbę pod znakiem logarytmu i podstawę logarytmu można łatwo przedstawić jako potęgę jakiejś liczby, bardzo wygodnie jest użyć wzoru , co odpowiada jednej z właściwości logarytmów. Rozważmy przykład znalezienia logarytmu, ilustrujący użycie tego wzoru.

Przykład.

Oblicz logarytm z .

Rozwiązanie.

Odpowiedź:

.

Właściwości logarytmów niewymienione powyżej są również wykorzystywane w obliczeniach, ale porozmawiamy o tym w kolejnych akapitach.

Znajdowanie logarytmów w kategoriach innych znanych logarytmów

Informacje zawarte w tym akapicie stanowią kontynuację tematu wykorzystania właściwości logarytmów do ich obliczania. Ale tutaj główna różnica polega na tym, że właściwości logarytmów są używane do wyrażenia oryginalnego logarytmu w kategoriach innego logarytmu, którego wartość jest znana. Weźmy przykład dla wyjaśnienia. Powiedzmy, że wiemy, że log 2 3≈1,584963 , możemy znaleźć na przykład log 2 6, wykonując małe przekształcenie z wykorzystaniem właściwości logarytmu: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

W powyższym przykładzie wystarczyło nam skorzystać z własności logarytmu iloczynu. Jednak znacznie częściej trzeba użyć szerszego arsenału właściwości logarytmów, aby obliczyć logarytm pierwotny na podstawie podanych.

Przykład.

Oblicz logarytm z 27 o podstawie 60, jeśli wiadomo, że log 60 2=a i log 60 5=b .

Rozwiązanie.

Musimy więc znaleźć log 60 27 . Łatwo zauważyć, że 27=3 3 , a pierwotny logarytm, ze względu na właściwość logarytmu stopnia, można zapisać jako 3·log 60 3 .

Zobaczmy teraz, jak log 60 3 można wyrazić za pomocą znanych logarytmów. Własność logarytmu liczby równej podstawie pozwala zapisać dziennik równości 60 60=1 . Z drugiej strony log 60 60=log60(2 2 3 5)= log 60 2 2 +log 60 3+log 60 5= 2 log 60 2+log 60 3+log 60 5 . Zatem, 2 log 60 2+log 60 3+log 60 5=1. Stąd, log 60 3=1−2 log 60 2−log 60 5=1−2 a−b.

Na koniec obliczamy oryginalny logarytm: log 60 27=3 log 60 3= 3 (1−2 a−b)=3−6 a−3 b.

Odpowiedź:

log 60 27=3 (1−2 a−b)=3−6 a−3 b.

Osobno warto wspomnieć o znaczeniu wzoru na przejście do nowej podstawy logarytmu postaci . Pozwala przejść od logarytmów o dowolnej podstawie do logarytmów o określonej podstawie, których wartości są znane lub możliwe jest ich znalezienie. Zwykle z oryginalnego logarytmu, zgodnie ze wzorem przejściowym, przechodzą na logarytmy w jednej z podstaw 2, e lub 10, ponieważ dla tych podstaw istnieją tabele logarytmów, które pozwalają na ich obliczenie z pewnym stopniem dokładności. W następnej sekcji pokażemy, jak to się robi.

Tablice logarytmów, ich zastosowanie

Do przybliżonego obliczenia wartości logarytmów można użyć tablice logarytmów. Najczęściej używane są tablica logarytmów o podstawie 2, tablica logarytmów naturalnych i tablica logarytmów dziesiętnych. Podczas pracy w systemie liczb dziesiętnych wygodnie jest użyć tabeli logarytmów o podstawie dziesiątej. Z jego pomocą nauczymy się znajdować wartości logarytmów.

Przedstawiona tablica pozwala z dokładnością do jednej dziesiątej tysięcznej znaleźć wartości logarytmów dziesiętnych liczb od 1.000 do 9.999 (z trzema miejscami po przecinku). Przeanalizujemy zasadę znajdowania wartości logarytmu za pomocą tabeli logarytmów dziesiętnych na konkretnym przykładzie - jest to jaśniejsze. Znajdźmy lg1,256 .

W lewej kolumnie tabeli logarytmów dziesiętnych znajdujemy pierwsze dwie cyfry liczby 1,256, czyli znajdujemy 1,2 (ta liczba jest zakreślona na niebiesko dla jasności). Trzecia cyfra liczby 1.256 (numer 5) znajduje się w pierwszym lub ostatnim wierszu na lewo od podwójnego wiersza (ta liczba jest zakreślona na czerwono). Czwarta cyfra pierwotnej liczby 1.256 (numer 6) znajduje się w pierwszym lub ostatnim wierszu na prawo od podwójnego wiersza (ta liczba jest zakreślona na zielono). Teraz znajdujemy liczby w komórkach tabeli logarytmów na przecięciu zaznaczonego wiersza i zaznaczonych kolumn (liczby te są podświetlone na pomarańczowo). Suma zaznaczonych liczb daje żądaną wartość logarytmu dziesiętnego do czwartego miejsca po przecinku, czyli log1,236≈0,0969+0,0021=0,0990.

Czy można, korzystając z powyższej tabeli, znaleźć wartości logarytmów dziesiętnych liczb, które mają więcej niż trzy cyfry po przecinku, a także wykraczają poza granice od 1 do 9,999? Tak, możesz. Pokażmy, jak to się robi na przykładzie.

Obliczmy lg102.76332 . Najpierw musisz napisać numer w standardowej formie: 102,76332=1,0276332 10 2 . Następnie mantysę należy zaokrąglić w górę do trzeciego miejsca po przecinku, mamy 1,0276332 10 2 ≈1,028 10 2, podczas gdy pierwotny logarytm dziesiętny jest w przybliżeniu równy logarytmowi liczby wynikowej, czyli bierzemy lg102,76332≈lg1,028·10 2 . Teraz zastosuj właściwości logarytmu: lg1.028 10 2 =lg1.028+lg10 2 =lg1.028+2. Ostatecznie znajdujemy wartość logarytmu lg1,028 zgodnie z tablicą logarytmów dziesiętnych lg1,028≈0,0086+0,0034=0,012. W rezultacie cały proces obliczania logarytmu wygląda następująco: lg102,76332=lg1,0276332 10 2 ≈lg1,028 10 2 = lg1,028+lg10 2 =lg1,028+2≈0,012+2=2,012.

Podsumowując, warto zauważyć, że korzystając z tabeli logarytmów dziesiętnych, można obliczyć przybliżoną wartość dowolnego logarytmu. Aby to zrobić, wystarczy użyć formuły przejścia, aby przejść do logarytmów dziesiętnych, znaleźć ich wartości w tabeli i wykonać pozostałe obliczenia.

Na przykład obliczmy log 2 3 . Zgodnie ze wzorem na przejście do nowej podstawy logarytmu mamy . Z tablicy logarytmów dziesiętnych znajdujemy lg3≈0,4771 i lg2≈0,3010. Zatem, .

Bibliografia.

• Kolmogorov A.N., Abramov AM, Dudnitsyn Yu.P. i inne Algebra i początki analizy: podręcznik dla klas 10-11 szkół ogólnokształcących.
• Gusiew VA, Mordkovich A.G. Matematyka (podręcznik dla kandydatów do techników).

Pojęcie logarytmu i podstawowa tożsamość logarytmiczna

Pojęcie logarytmu i podstawowa tożsamość logarytmiczna są ze sobą ściśle powiązane, ponieważ definicja logarytmu w notacja matematyczna i jest .

Podstawowa tożsamość logarytmiczna wynika z definicji logarytmu:

Definicja 1

logarytm wywołaj wykładnik $n$, po podniesieniu którego liczby $a$ dostaną liczbę $b$.

Uwaga 1

równanie wykładnicze$a^n=b$ dla $a > 0$, $a \ne 1$ nie ma rozwiązań dla niedodatnich $b$ i ma pojedynczy pierwiastek dla dodatniego $b$. Ten korzeń nazywa się logarytm liczby $b$ do podstawy $a$ i napisz:

$a^(\log_(a) b)=b$.

Definicja 2

Wyrażenie

$a^(\log_(a) b)=b$

zwany podstawowa tożsamość logarytmiczna pod warunkiem, że $a,b > 0$, $a \ne 1$.

Przykład 1

$17^(\log_(17) 6)=6$;

$e^(\ln⁡13) =13$;

$10^(\lg23)=23$.

Podstawowa tożsamość logarytmiczna

Główny tożsamość logarytmiczna nazywana jest ponieważ jest prawie zawsze używany podczas pracy z logarytmami. Ponadto za jego pomocą uzasadnione są podstawowe właściwości logarytmów.

Przykład 2

$7^5=16 807$, stąd $\log_(7)16 807=5$.

$3^(-5)=\frac(1)(243)$, stąd $\log_(3)\frac(1)(243)=-5$.

$11^0=1$, stąd $\log_(11)⁡1=0$.

Rozważać konsekwencja podstawowej tożsamości logarytmicznej:

Definicja 3

Jeśli dwa logarytmy o tej samej podstawie są równe, to wyrażenia logarytmiczne są równe:

jeśli $\log_(a)⁡b=\log_(a)⁡c$, to $b=c$.

Rozważać ograniczenia, które są używane do tożsamości logarytmicznej:

Ponieważ podnosząc jedynkę do dowolnej potęgi, zawsze otrzymujemy jedynkę, a równość $x=\log_(a)⁡b$ istnieje tylko dla $b=1$, wtedy $\log_(1)⁡1$ będzie dowolne prawdziwy numer. Aby uniknąć tej dwuznaczności, przyjmuje się, że $a \ne 1$.

Zgodnie z definicją logarytm dla $a=0$ może istnieć tylko dla $b=0$. Ponieważ podnosząc zero do dowolnej potęgi, zawsze otrzymujemy zero, wtedy $\log_(0)⁡0$ może być dowolną liczbą rzeczywistą. Aby uniknąć tej dwuznaczności, zakłada się, że $a \ne 0$. Dla racjonalnego i irracjonalny wartości logarytmiczne, ponieważ stopień z wykładnikiem wymiernym i niewymiernym można obliczyć tylko dla dodatnich podstaw. Aby zapobiec takiej sytuacji, akceptowane jest $a > 0$.

$b > 0$ wynika z warunku $a > 0$, ponieważ $x=\log_(a)⁡b$, a potęga liczby dodatniej a zawsze będzie dodatnia.

Podstawowa tożsamość logarytmiczna jest często używana do uproszczenia wyrażeń logarytmicznych.

Przykład 3

Oblicz 81 $^(\log_(9) 7)$.

Rozwiązanie.

Aby móc korzystać z podstawowej tożsamości logarytmicznej, podstawa logarytmu i wykładnik muszą być takie same. Piszemy podstawę stopnia w postaci:

Teraz możemy napisać:

$81^(\log_(9)7)=(9^2)^(\log_(9)7)=$

Skorzystajmy z własności stopnia:

$=9^(2 \cdot \log_(9)7)=9^(\log_(9)7) \cdot 9^(\log_(9)7)=$

podstawową tożsamość logarytmiczną można teraz zastosować do każdego czynnika:

$=7 \cdot 7=49$.

Uwaga 2

Aby zastosować podstawową tożsamość logarytmiczną, możesz również skorzystać z zastąpienia podstawy logarytmu wyrażeniem znajdującym się pod znakiem logarytmu i odwrotnie.

Przykład 4

Oblicz 7 $^(\frac(1)(\log_(11) 7))$.

Rozwiązanie.

$7^(\frac(1)(\log_(11) 7))=7^(\log_(7) 11)=11$.

Odpowiedź: $11$.

Przykład 5

Oblicz 7 $^(\frac(3)(\log_(11) 7))$.