Пријавете се по основа. Дефиниција на логаритамот и неговите својства: теорија и решавање проблеми

(од грчки λόγος - „збор“, „врска“ и ἀριθμός - „број“) броеви ббазирано на а(лога α б) се нарекува таков број в, И б= а в, односно го запишува дневникот α б=вИ b=aвсе еквивалентни. Логаритмот има смисла ако a > 0, a ≠ 1, b > 0.

Со други зборови логаритамброеви ббазирано на Аформулиран како експонент на кој мора да се подигне број аза да го добиете бројот б(логаритам постои само за позитивни броеви).

Од оваа формулација произлегува дека пресметката x= log α б, е еквивалентно на решавање на равенката a x =b.

На пример:

дневник 2 8 = 3 бидејќи 8 = 2 3 .

Да нагласиме дека посочената формулација на логаритамот овозможува веднаш да се определи логаритамска вредност, кога бројот под знакот логаритам делува како одредена моќност на основата. Навистина, формулацијата на логаритмот овозможува да се оправда дека ако b=a c, потоа логаритам на бројот ббазирано на аеднакви Со. Исто така, јасно е дека темата логаритми е тесно поврзана со темата моќи на број.

Пресметувањето на логаритам се нарекува логаритам. Логаритам е математичка операција на земање логаритам. Кога се земаат логаритми, производите на факторите се трансформираат во збирови на членови.

Потенцијацијае инверзна математичка операција на логаритам. За време на потенцирањето, дадена основа се подига до степенот на изразување над кој се врши потенцирањето. Во овој случај, збировите на поими се трансформираат во производ на фактори.

Доста често, реалните логаритми се користат со основите 2 (бинарни), Ојлеровиот број e ≈ 2,718 (природен логаритам) и 10 (децимална).

На на оваа бинапрепорачливо е да се разгледа логаритамски примероцидневник 7 2 , ln √ 5, lg0,0001.

И записите lg(-3), log -3 3.2, log -1 -4.3 немаат смисла, бидејќи во првиот од нив негативен број се става под знакот логаритам, во вториот - негативен бројво основата, а во третата - и негативен број под знакот на логаритам и единица во основата.

Услови за определување на логаритам.

Вреди да се разгледаат одделно условите a > 0, a ≠ 1, b > 0.под кои добиваме дефиниција на логаритам.Ајде да размислиме зошто беа преземени овие ограничувања. Во тоа ќе ни помогне еднаквоста од формата x = log α б, наречен основен логаритамски идентитет, што директно произлегува од дефиницијата за логаритам дадена погоре.

Да ја земеме состојбата a≠1. Бидејќи еден на која било моќност е еднаков на еден, тогаш еднаквоста x=log α бможе да постои само кога b=1, но дневникот 1 1 ќе биде кој било реален број. За да ја елиминираме оваа нејасност, земаме a≠1.

Да ја докажеме неопходноста на состојбата a>0. На a=0според формулацијата на логаритамот може да постои само кога b=0. И соодветно тогаш дневник 0 0може да биде кој било реален број што не е нула, бидејќи нула до која било ненулта моќност е нула. Оваа двосмисленост може да се отстрани со состојбата a≠0. И кога а<0 би требало да ја отфрлиме анализата на рационалните и ирационалните вредности на логаритмот, бидејќи степенот со рационален и ирационален експонент е дефиниран само за ненегативни основи. Токму поради оваа причина условот е пропишан a>0.

И последниот услов б>0произлегува од нееднаквоста a>0, бидејќи x=log α б, и вредноста на степенот со позитивна основа асекогаш позитивно.

Карактеристики на логаритмите.

Логаритмисе карактеризира со карактеристични карактеристики, што доведе до нивна широка употреба за значително олеснување на макотрпните пресметки. Кога се движите „во светот на логаритмите“, множењето се трансформира во многу полесно собирање, делењето се трансформира во одземање, а степенувањето и извлекувањето на коренот се трансформираат, соодветно, во множење и делење со експонентот.

Формулацијата на логаритми и табела на нивните вредности (за тригонометриски функции) за прв пат беше објавена во 1614 година од шкотскиот математичар Џон Напиер. Логаритамските табели, зголемени и детални од други научници, беа широко користени во научните и инженерските пресметки и останаа релевантни до употребата на електронски калкулатори и компјутери.

Дефиниција на логаритам

Логаритмот од b до основата a е експонентот до кој мора да се подигне a за да се добие b.

Број дво математиката вообичаено е да се означи границата до која се стреми изразот

Број де ирационален број- број неспоредлив со еден, не може точно да се изрази ниту како цел број ниту како дропка рационаленброј.

Писмо д- прва буква од латински збор изложувач- да се покаже, па оттука и името во математиката експоненцијален- експоненцијална функција.

Број дшироко користен во математиката, и во сите науки кои на еден или друг начин користат математички пресметки за своите потреби.

Логаритми. Својства на логаритмите

Дефиниција: Логаритмот на позитивен број b на неговата основа е експонентот c на кој мора да се подигне бројот a за да се добие бројот b.

Основен логаритамски идентитет:

7) Формула за преселба во нова база:

lna = log e a, e ≈ 2,718…

Задачи и тестови на тема „Логаритми. Својства на логаритмите“

• Логаритми - Важни теми за прегледување на Единствениот државен испит по математика

За успешно завршување на задачите на оваа тема, мора да ја знаете дефиницијата за логаритам, својствата на логаритмите, основниот логаритамски идентитет, дефинициите за децимални и природни логаритми. Главните типови на проблеми на оваа тема се проблеми кои вклучуваат пресметување и трансформација на логаритамски изрази. Да го разгледаме нивното решение користејќи ги следните примери.

Решение:Користејќи ги својствата на логаритмите, добиваме

Решение:Користејќи ги својствата на степените, добиваме

1) (2 2) дневник 2 5 =(2 дневник 2 5) 2 =5 2 =25

Својства на логаритми, формулации и докази.

Логаритмите имаат голем број на карактеристични својства. Во оваа статија ќе ги разгледаме главните својства на логаритми. Овде ќе ги дадеме нивните формулации, ќе ги запишеме својствата на логаритмите во форма на формули, ќе покажеме примери за нивната примена, а исто така ќе обезбедиме доказ за својствата на логаритмите.

Навигација на страницата.

Основни својства на логаритмите, формули

За полесно запомнување и користење, ајде да замислиме основни својства на логаритмитево форма на листа на формули. Во следниот пасус ќе ги дадеме нивните формулации, докази, примери за употреба и потребни објаснувања.

Својство на логаритамот на единство: log a 1=0 за кое било a>0, a≠1.

Логаритм на број, еднаква на основата: log a a=1 за a>0, a≠1.

Својство на логаритамот на моќноста на основата: log a a p =p, каде што a>0, a≠1 и p е секој реален број.

Логаритам на производот од два позитивни броја: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
и својството на логаритамот на производот од n позитивни броеви: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, ..., x n >0.

Својство на логаритам на количник: , каде што a>0, a≠1, x>0, y>0.

Логаритам на моќноста на број: log a b p =p·log a |b| , каде што a>0, a≠1, b и p се броеви такви што степенот b p има смисла и b p >0.

Последица: , каде a>0, a≠1, n - природен број, поголемо од еден, b>0.

Заклучок 1: , a>0, a≠1, b>0, b≠1.

Заклучок 2: , a>0 , a≠1 , b>0 , p и q се реални броеви, q≠0 , особено за b=a имаме .

Формулации и докази за својства

Продолжуваме со формулација и докажување на пишаните својства на логаритмите. Сите својства на логаритмите се докажуваат врз основа на дефиницијата на логаритмот и основниот принцип што произлегува од него логаритамски идентитет, како и својствата на степенот.

Да почнеме со својства на логаритмот на еден. Неговата формулација е како што следува: логаритамот на единство е еднаков на нула, т.е. логирајте 1=0за кое било a>0, a≠1. Доказот не е тежок: бидејќи a 0 =1 за кој било a ги задоволува горенаведените услови a>0 и a≠1, тогаш логот за еднаквост a 1=0 што треба да се докаже следи веднаш од дефиницијата на логаритамот.

Да дадеме примери за примена на разгледуваното својство: log 3 1=0, log1=0 и .

Ајде да продолжиме на следниот имот: логаритамот на број еднаков на основата е еднаков, тоа е, log a a=1за a>0, a≠1. Навистина, бидејќи a 1 =a за кое било a, тогаш по дефиниција на логаритамот log a a=1.

Примери за користење на ова својство на логаритми се равенките log 5 5=1, log 5.6 5.6 и lne=1.

Логаритмот на моќта на број еднаков на основата на логаритамот е еднаков на експонентот. Ова својство на логаритмот одговара на формулата на формата log a a p =p, каде што a>0, a≠1 и p – кој било реален број. Ова својство произлегува директно од дефиницијата на логаритамот. Забележете дека ви овозможува веднаш да ја означите вредноста на логаритмот, ако е можно да се претстави бројот под знакот на логаритам како моќност на основата; ќе зборуваме повеќе за ова во написот за пресметување логаритми.

На пример, log 2 2 7 =7, log10 -4 =-4 и .

Логаритам на производот од два позитивни броја x и y еднаков на производотлогаритми на овие броеви: log a (x y)=log a x+log a y, a>0, a≠1. Дозволете ни да го докажеме својството на логаритмот на производот. Поради својствата на степенот a log a x+log a y =a log a x ·a log a y, и бидејќи според главниот логаритамски идентитет log a x =x и лог a y =y, тогаш лог a x ·a log a y =x· y. Така, лог a x+log a y =x·y, од кој, според дефиницијата на логаритам, следи еднаквоста што се докажува.

Да покажеме примери за користење на својството на логаритам на производ: log 5 (2 3)=log 5 2+log 5 3 и .

Својството на логаритмот на производ може да се генерализира на производот на конечен број n од позитивни броеви x 1 , x 2 , …, x n како log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Оваа еднаквост може да се докаже без проблеми со користење на методот на математичка индукција.

На пример, природниот логаритам на производот може да се замени со збир од три природни логаритми од броевите 4, e и.

Логаритам на количник на два позитивни броја x и y е еднаква на разликата помеѓу логаритмите на овие броеви. Својството на логаритамот на количник одговара на формулата на формата , каде што a>0, a≠1, x и y се некои позитивни броеви. Се докажува валидноста на оваа формула како и формулата за логаритам на производ: бидејќи , потоа по дефиниција на логаритам .

Еве пример за користење на ова својство на логаритмот: .

Ајде да продолжиме на својство на логаритмот на моќноста. Логаритмот на степен е еднаков на производот на експонентот и логаритамот на модулот на основата на овој степен. Да го напишеме ова својство на логаритмот на моќта како формула: log a b p =p·log a |b|, каде што a>0, a≠1, b и p се броеви такви што степенот b p има смисла и b p >0.

Прво го докажуваме ова својство за позитивно б. Основниот логаритамски идентитет ни овозможува да го претставиме бројот b како лог a b , потоа b p =(a log a b) p , а добиениот израз, поради својството на моќ, е еднаков на p·log a b . Значи, доаѓаме до еднаквоста b p =a p·log a b, од која, според дефиницијата за логаритам, заклучуваме дека log a b p =p·log a b.

Останува да се докаже ова својство за негативно б. Овде забележуваме дека изразот log a b p за негативно b има смисла само за парни експоненти p (бидејќи вредноста на степенот b p мора да биде поголема од нула, во спротивно логаритамот нема да има смисла), а во овој случај b p =|b| стр. Тогаш b p =|b| p =(a log a |b|) p =a p·log a |b| , од каде log a b p =p·log a |b| .

На пример, и ln(-3) 4 =4·ln|-3|=4·ln3.

Тоа произлегува од претходниот имот својство на логаритмот од коренот: логаритамот на n-тиот корен е еднаков на производот на дропот 1/n со логаритамот на радикалниот израз, односно каде a>0, a≠1, n е природен број поголем од еден, b>0 .

Доказот се заснова на еднаквоста (види дефиниција за експонент со фракционо експонент), која важи за секој позитивен b, и својството на логаритамот на експонентот: .

Еве пример за користење на ова својство: .

Сега да докажеме формула за преминување во нова логаритамска основаљубезен . За да го направите ова, доволно е да се докаже валидноста на логот за еднаквост c b=log a b·log c a. Основниот логаритамски идентитет ни овозможува да го претставиме бројот b како лог a b , потоа log c b=log c a log a b . Останува да се користи својството на логаритамот на степенот: log c a log a b =log a b·log c a . Ова ја докажува еднаквоста log c b=log a b·log c a, што значи дека е докажана и формулата за премин кон нова основа на логаритамот .

Да покажеме неколку примери за користење на ова својство на логаритми: и .

Формулата за преместување во нова база ви овозможува да продолжите да работите со логаритми кои имаат „погодна“ основа. На пример, може да се користи за промена на природни или децимални логаритми за да можете да ја пресметате вредноста на логаритам од табела со логаритми. Формулата за преместување во нова логаритамска основа, исто така, овозможува, во некои случаи, да се најде вредноста на даден логаритам кога се познати вредностите на некои логаритми со други основи.

Се користи често посебен случајформули за премин кон нова основа на логаритамот со c=b од формата. Ова покажува дека log a b и log b a се меѓусебно инверзни броеви. На пр. .

Често се користи и формулата, што е погодно за пронаоѓање на вредностите на логаритмите. За да ги потврдиме нашите зборови, ќе покажеме како може да се користи за пресметување на вредноста на логаритам на формата. Ние имаме . За да се докаже формулата, доволно е да се користи формулата за преместување во нова основа на логаритмот a: .

Останува да се докажат својствата на споредување на логаритмите.

Ајде да го користиме спротивниот метод. Да претпоставиме дека за 1 >1, a 2 >1 и a 1 2 и за 0 1, log a 1 b≤log a 2 b е точно. Врз основа на својствата на логаритмите, овие неравенки може да се препишат како И соодветно, и од нив следува дека log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2, соодветно. Потоа, според својствата на моќите со по истите основимора да се задоволат еднаквостите b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2, односно a 1 ≥a 2 . Така, дојдовме до контрадикција со условот a 1 2. Ова го комплетира доказот.

Основни својства на логаритмите

• Материјали за лекцијата
• Преземете ги сите формули

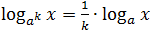
Логаритмите, како и сите броеви, можат да се собираат, одземаат и трансформираат на секој начин. Но, бидејќи логаритмите не се баш обични броеви, тука постојат правила, кои се нарекуваат главните својства.

Дефинитивно треба да ги знаете овие правила - без нив не може да се реши ниту еден сериозен логаритамски проблем. Покрај тоа, има многу малку од нив - можете да научите сè за еден ден. Па ајде да започнеме.

Собирање и одземање логаритми

Размислете за два логаритма со исти основи: log a x и log a y. Потоа тие можат да се собираат и одземаат и:

Значи, збирот на логаритми е еднаков на логаритмот на производот, а разликата е еднаква на логаритмот на количникот. Забелешка: клучен моментЕве - идентични основи. Ако причините се различни, овие правила не функционираат!

Овие формули ќе ви помогнат да пресметате логаритамски израз дури и кога неговите поединечни делови не се разгледуваат (видете ја лекцијата „Што е логаритам“). Погледнете ги примерите и видете:

Задача. Најдете ја вредноста на изразот: log 6 4 + log 6 9.

Бидејќи логаритмите имаат исти основи, ја користиме формулата за збир:
дневник 6 4 + дневник 6 9 = дневник 6 (4 9) = дневник 6 36 = 2.

Задача. Најдете ја вредноста на изразот: log 2 48 − log 2 3.

Основите се исти, ја користиме формулата за разлика:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Најдете ја вредноста на изразот: log 3 135 − log 3 5.

Повторно, основите се исти, така што имаме:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Како што можете да видите, оригиналните изрази се составени од „лоши“ логаритми, кои не се пресметуваат одделно. Но, по трансформациите тие излегуваат доста нормални бројки. Многумина се изградени на овој факт тест трудови. Да, изразите слични на тестот се нудат со сета сериозност (понекогаш практично без промени) на унифицираниот државен испит.

Извлекување на експонентот од логаритамот

Сега да ја комплицираме задачата малку. Што ако основата или аргументот на логаритам е моќност? Тогаш експонентот на овој степен може да се извади од знакот на логаритамот според следниве правила:

• log a x n = n · log a x ;
• 
• 

Тоа е лесно да се забележи последното правилоследи првите две. Но, во секој случај, подобро е да се запамети - во некои случаи значително ќе го намали износот на пресметките.

Се разбира, сите овие правила имаат смисла ако се почитува ODZ на логаритмот: a > 0, a ≠ 1, x > 0. И уште една работа: научете да ги применувате сите формули не само од лево кон десно, туку и обратно , т.е. Можете да ги внесете броевите пред знакот за логаритам во самиот логаритам. Ова е она што најчесто се бара.

Задача. Најдете ја вредноста на изразот: log 7 49 6 .

Ајде да се ослободиме од степенот во аргументот користејќи ја првата формула:
дневник 7 49 6 = 6 дневник 7 49 = 6 2 = 12

Задача. Најдете го значењето на изразот:

[Наслов за сликата]

Забележете дека именителот содржи логаритам, чија основа и аргумент се точни моќи: 16 = 2 4 ; 49 = 7 2. Ние имаме:

[Наслов за сликата]

Мислам дека последниот пример бара некое појаснување. Каде отидоа логаритмите? До последен момент работиме само со именителот. Ја претставивме основата и аргументот на логаритмот што стои таму во форма на моќности и ги извадивме експонентите - добивме дропка „три ката“.

Сега да ја погледнеме главната фракција. Броителот и именителот го содржат истиот број: log 2 7. Бидејќи log 2 7 ≠ 0, можеме да ја намалиме дропката - 2/4 ќе остане во именителот. Според правилата на аритметиката, четворката може да се пренесе на броителот, што е направено. Резултатот беше одговорот: 2.

Транзиција кон нова основа

Зборувајќи за правилата за собирање и одземање логаритми, конкретно нагласив дека тие работат само со исти основи. Што ако причините се различни? Што ако тие не се точни моќи со ист број?

На помош доаѓаат формулите за транзиција кон нова основа. Да ги формулираме во форма на теорема:

Нека е даден логаритамскиот лог a x. Тогаш за кој било број c таков што c > 0 и c ≠ 1, еднаквоста е точно:

[Наслов за сликата]

Конкретно, ако поставиме c = x, добиваме:

[Наслов за сликата]

Од втората формула произлегува дека основата и аргументот на логаритмот може да се заменат, но во овој случај целиот израз е „превртен“, т.е. логаритмот се појавува во именителот.

Овие формули ретко се наоѓаат во обичните нумерички изрази. Можно е да се оцени колку се погодни само со одлучување логаритамски равенкии нееднаквости.

Сепак, има проблеми кои не можат да се решат воопшто освен со преселба во нова основа. Ајде да погледнеме неколку од овие:

Задача. Најдете ја вредноста на изразот: log 5 16 log 2 25.

Забележете дека аргументите на двата логаритма содржат точни моќи. Ајде да ги извадиме индикаторите: лог 5 16 = дневник 5 2 4 = 4лог 5 2; дневник 2 25 = дневник 2 5 2 = 2 дневник 2 5;

Сега да го „превртиме“ вториот логаритам:

[Наслов за сликата]

Бидејќи производот не се менува при преуредување фактори, мирно помноживме четири и два, а потоа се занимававме со логаритми.

Задача. Најдете ја вредноста на изразот: log 9 100 lg 3.

Основата и аргументот на првиот логаритам се точни моќи. Ајде да го запишеме ова и да се ослободиме од индикаторите:

[Наслов за сликата]

Сега да се ослободиме од децималниот логаритам со преместување во нова основа:

[Наслов за сликата]

Основен логаритамски идентитет

Често во процесот на решавање е потребно да се претстави број како логаритам на дадена основа. Во овој случај, следните формули ќе ни помогнат:

1. n = log a a n

2. Во првиот случај, бројот n станува експонент во аргументот. Бројот n може да биде апсолутно се, бидејќи е само логаритамска вредност.

   Втората формула е всушност парафразирана дефиниција. Така се нарекува: основен логаритамски идентитет.

   Всушност, што ќе се случи ако бројот b се подигне до таква моќ што бројот b на оваа моќност го дава бројот a? Така е: резултатот е ист број a. Прочитајте го овој пасус повторно внимателно - многу луѓе се заглавуваат на него.

   Како формули за преместување во нова основа, основниот логаритамски идентитет понекогаш е единственото можно решение.

   [Наслов за сликата]

   Забележете дека log 25 64 = log 5 8 - едноставно го зедовме квадратот од основата и аргументот на логаритамот. Земајќи ги предвид правилата за множење моќи со иста основа, добиваме:

   [Наслов за сликата]

   Ако некој не знае, ова беше вистинска задача од Единствениот државен испит :)

   Логаритамска единица и логаритамска нула

   Како заклучок, ќе дадам два идентитети кои тешко можат да се наречат својства - напротив, тие се последици од дефиницијата на логаритамот. Тие постојано се појавуваат во проблеми и изненадувачки им создаваат проблеми дури и на „напредните“ студенти.

   1. log a a = 1 е логаритамска единица. Запомнете еднаш засекогаш: логаритамот на која било основа a од самата основа е еднаков на еден.
   2. log a 1 = 0 е логаритамска нула. Основата a може да биде што било, но ако аргументот содржи еден, логаритамот е еднаков на нула! Бидејќи 0 = 1 е директна последица на дефиницијата.

   Тоа се сите својства. Задолжително вежбајте да ги применувате во пракса! Преземете го мамечкиот лист на почетокот на лекцијата, испечатете го и решете ги проблемите.

   Логаритам. Својства на логаритмот (собирање и одземање).

   Својства на логаритмотследи од неговата дефиниција. И така логаритамот на бројот ббазирано на Асе дефинира како експонент до кој мора да се подигне број аза да го добиете бројот б(логаритам постои само за позитивни броеви).

   Од оваа формулација произлегува дека пресметката x=log a b, е еквивалентно на решавање на равенката a x =b.На пример, дневник 2 8 = 3бидејќи 8 = 2 3 . Формулирањето на логаритмот овозможува да се оправда дека ако b=a c, потоа логаритам на бројот ббазирано на аеднакви Со. Исто така, јасно е дека темата логаритми е тесно поврзана со темата за моќи.

   Со логаритми, како и со сите броеви, можете да направите операции собирање, одземањеи да се трансформираат на секој можен начин. Но, поради фактот што логаритмите не се сосема обични броеви, овде важат нивните посебни правила, кои се нарекуваат главните својства.

   Собирање и одземање логаритми.

   Да земеме два логаритами со исти основи: логирајте xИ најавите y. Тогаш е можно да се извршат операции за собирање и одземање:

   Како што гледаме, збир на логаритмие еднаков на логаритмот на производот, и разлика логаритми- логаритам на количникот. Покрај тоа, ова е точно ако бројките А, ХИ напозитивни и a ≠ 1.

   Важно е да се напомене дека главниот аспект во овие формули се истите основи. Ако основите се различни, овие правила не важат!

   Правилата за собирање и одземање логаритми со исти основи се читаат не само од лево кон десно, туку и обратно. Како резултат на тоа, ги имаме теоремите за логаритам на производот и логаритам на количникот.

   Логаритам на производотдва позитивни броја е еднаква на збирот на нивните логаритми ; преформулирајќи ја оваа теорема го добиваме следново ако броевите А, xИ напозитивни и a ≠ 1, Тоа:

   Логаритам на количникотдва позитивни броја е еднаква на разликата помеѓу логаритмите на дивидендата и делителот. Поинаку кажано, ако бројките А, XИ напозитивни и a ≠ 1, Тоа:

   Да ги примениме горенаведените теореми за решавање примери:

   Доколку бројките xИ натогаш се негативни формула за логаритам на производотстанува бесмислено. Така, забрането е да се напише:

   бидејќи изразите log 2 (-8) и log 2 (-4) воопшто не се дефинирани (логаритамска функција на= дневник 2 Xдефинирани само за позитивни вредности на аргументи X).

   Теорема на производотприменливо не само за два, туку и за неограничен број фактори. Тоа значи дека за секој природен ки сите позитивни бројки x 1 , x 2 , . . . ,x nима идентитет:

   Од Теорема за логаритамски количникМоже да се добие уште едно својство на логаритмот. Општо познато е дека дневникот а 1= 0, значи

   Ова значи дека постои еднаквост:

   Логаритми од два реципрочни бројаод истата причина ќе се разликуваат едни од други исклучиво по знак. Значи:

   Логаритам. Својства на логаритмите

   Логаритам. Својства на логаритмите

   Ајде да размислиме за еднаквоста. Дозволете ни да ги знаеме вредностите на и и сакаме да ја најдеме вредноста на.

   Односно, ние го бараме експонентот со кој треба да го затегнеме за да го добиеме.

   Нека променливата може да земе која било вистинска вредност, тогаш на променливите им се наметнуваат следните ограничувања: o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″ />

   Ако ги знаеме вредностите на и, а сме соочени со задача да го најдеме непознатото, тогаш за таа цел се воведува математичка операција, која се нарекува. логаритам.

   За да ја најдеме вредноста што ја земаме логаритам на бројОд страна на основа :

   Логаритмот на еден број до неговата основа е експонентот до кој мора да се подигне за да се добие .

   Тоа е основен логаритамски идентитет:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   во суштина е математичка нотација дефиниции за логаритам.

   Математичката операција на логаритам е инверзна на операцијата на степенување, така својства на логаритмисе тесно поврзани со својствата на степенот.

   Да ги наведеме главните својства на логаритми:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ наслов=”d1″/>

   4.

   5.

   Следната група својства ви овозможува да го претставите експонентот на изразот под знакот на логаритам или да стои на основата на логаритамот во форма на коефициент пред знакот на логаритамот:

   6.

   7.

   8.

   9.

   Следната група формули ви овозможува да преминете од логаритам со дадена основа во логаритам со произволна основа, и се нарекува формули за премин кон нова база:

   10.

   12. (заклучок од имотот 11)

   

   Следниве три својства не се добро познати, но тие често се користат при решавање на логаритамски равенки или при поедноставување на изрази што содржат логаритми:

   13.

   14.

   15.

   Посебни случаи:

   — децимален логаритам

   — природен логаритам

   При поедноставување на изрази кои содржат логаритми, се користи општ пристап:

   1. Воведување децималиво форма на обични.

   2. Мешани броевипретставени како неправилни дропки.

   3. Броевите во основата на логаритамот и под знакот на логаритамот ги разложуваме на едноставни фактори.

   4. Се обидуваме да ги намалиме сите логаритми на иста основа.

   5. Примени ги својствата на логаритмите.

   Ајде да погледнеме примери за поедноставување на изрази кои содржат логаритми.

   Пример 1.

   Пресметајте:

   Ајде да ги поедноставиме сите експоненти: нашата задача е да ги сведеме на логаритми, чија основа е ист број како и основата на експонентот.

   ==(по својство 7)=(по својство 6) =

   Ајде да ги замениме индикаторите што ги најдовме во оригиналниот израз. Добиваме:

   Одговор: 5.25

   Пример 2. Пресметајте:

   

   Ајде да ги намалиме сите логаритми на основата 6 (во овој случај, логаритмите од именителот на дропката ќе „мигрираат“ до броителот):

   Ајде да ги разложиме броевите под знакот логаритам на едноставни фактори:

   Ајде да ги примениме својствата 4 и 6:

   Ајде да ја претставиме замената

   Добиваме:

   Одговор: 1

   Логаритам . Основен логаритамски идентитет.

   Својства на логаритмите. Децимален логаритам. Природен логаритам.

   Логаритам позитивен број N до основата (б > 0, б 1) е експонентот x до кој b мора да се подигне за да се добие N .

   Овој запис е еквивалентен на следново: b x = N .

   Примери: дневник 3 81 = 4, бидејќи 3 4 = 81;

   дневник 1/3 27 = – 3, бидејќи (1/3) - 3 = 3 3 = 27.

   Горенаведената дефиниција за логаритам може да се напише како идентитет:

   

   Основни својства на логаритмите.

   2) дневник 1 = 0, бидејќи б 0 = 1 .

   3) Логаритмот на производот е еднаков на збирот на логаритмите на факторите:

   4) Логаритмот на количникот е еднаков на разликата помеѓу логаритмите на дивидендата и делителот:

   5) Логаритмот на моќноста е еднаков на производот на експонентот и логаритамот на неговата основа:

   Последица на ова својство е следново: логаритам на коренот еднаков на логаритамрадикален број поделен со моќноста на коренот:

   

   6) Ако основата на логаритмот е степен, тогаш вредноста инверзната на експонентот може да се извади како дневничка рима:

   

   Последните две својства може да се комбинираат во едно:

   

   7) Формула за преодниот модул (т.е. премин од една логаритамска основа во друга база):

   

   Во посебниот случај кога N=aние имаме:

   

   Децимален логаритам повикани основен логаритам 10. Се означува лг, т.е. дневник 10 Н= дневник Н. Логаритми на броеви 10, 100, 1000, . стр се 1, 2, 3, ..., соодветно, т.е. има толку многу позитивни

   единици, колку нули има во логаритамски број после една. Логаритми на броеви 0,1, 0,01, 0,001, . p се соодветно –1, –2, –3, …, т.е. имаат толку негативни колку што има нули во логаритамскиот број пред еден (вклучувајќи нула цели броеви). Логаритмите на другите броеви имаат фракционен дел наречен мантиса. Целиот дел од логаритам се нарекува карактеристика. За практична употреба, децималните логаритми се најпогодни.

   Природен логаритам повикани основен логаритам д. Се означува со ln, т.е. дневник д Н= дневник Н. Број де ирационален, неговата приближна вредност е 2,718281828. Тоа е границата кон која бројот се стреми (1 + 1 / n) nсо неограничено зголемување n(цм. прво прекрасна граница на страницата „Граници“. секвенци на броеви»).
   Колку и да изгледа чудно, природните логаритми се покажаа како многу погодни при извршување на разни видови операции поврзани со анализа на функции. Пресметување логаритми до база дсе врши многу побрзо отколку поради која било друга причина.

• Што е потребно денес за посвојување дете во Русија? Усвојувањето во Русија, покрај одговорната лична одлука, вклучува и голем број процедури за државна верификација на кандидатите. Тешка селекција за подготвителна фазапридонесува за повеќе […]
• Бесплатни информации за TIN или OGRN од даночниот регистар низ цела Русија - онлајн Информации за државна регистрација може да се добијат на порталот за унифицирани даночни услуги правни лица, индивидуални претприемачи, […]
• Казна за возење без документи (возачка дозвола, осигурување, СТС) Понекогаш, поради заборав, возачите седнуваат зад воланот без дозвола и добиваат казна за возење без документи. Да потсетиме, автомобилскиот ентузијаст вози со своите задолжително […]
• Цвеќиња за мажи. Какви цвеќиња можете да му дадете на мажот? Какви цвеќиња можете да му дадете на мажот? Нема многу „машки“ цвеќиња, но има и такви што им се даваат на мажите. Мала цветна листа пред вас: Хризантеми. Рози. Каранфили. […]
• Меморандум за услугае посебна форма на документ што се користи во внатрешно опкружувањепретпријатија и служи за брзо решавање на тековните производствени проблеми. Обично овој документ се составува со цел да се воведат некои […]
• Кога и како да го добиете финансираниот дел од вашата пензија од Сбербанк? Сбербанк е партнерска банка на државниот пензиски фонд. Врз основа на ова, граѓаните кои се пријавиле за финансирана пензија може да го префрлат финансираниот дел […]
• Детски бенефиции во Улјановск и регионот Уљановск во 2018 година Покрај тоа, програмите одобрени со федералното законодавство функционираат во сите региони. Ајде да погледнеме кој може да смета на какви придобивки. Како регионалните власти […]
• Детален водич за тоа како да се состави полномошно за застапување на интереси индивидуалнана суд Во граѓанско или арбитражно барање, во административен или кривичен случај, интересите и на тужителот и на обвинетиот можат да бидат застапувани од адвокат: […]

Инструкции

Напиши го дадениот логаритамски израз. Ако изразот користи логаритам од 10, тогаш неговата нотација е скратена и изгледа вака: lg b е декаден логаритам. Ако логаритамот го има како основа бројот e, тогаш напиши го изразот: ln b – природен логаритам. Разбирливо е дека резултатот од било која е моќноста до која мора да се подигне основниот број за да се добие бројот b.

Кога го наоѓате збирот на две функции, едноставно треба да ги разликувате една по една и да ги додадете резултатите: (u+v)" = u"+v";

При наоѓање на изводот на производот на две функции, потребно е да се помножи изводот на првата функција со втората и да се додаде изводот на втората функција помножен со првата функција: (u*v)" = u"*v +v"*u;

За да се најде изводот на количникот на две функции, потребно е да се одземе од производот на изводот на дивидендата помножен со функцијата на делител, производот од изводот на делителот помножен со функцијата на дивидендата и да се подели сето тоа со функцијата делител на квадрат. (u/v)" = (u"*v-v"*u)/v^2;

Доколку се дадени комплексна функција, тогаш потребно е да се помножи изводот на внатрешна функцијаа дериватот на надворешниот. Нека y=u(v(x)), потоа y"(x)=y"(u)*v"(x).

Користејќи ги резултатите добиени погоре, можете да разликувате речиси секоја функција. Значи, да погледнеме неколку примери:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
Исто така, има проблеми со пресметување на изводот во одредена точка. Нека е дадена функцијата y=e^(x^2+6x+5), треба да ја пронајдете вредноста на функцијата во точката x=1.
1) Најдете го изводот на функцијата: y"=e^(x^2-6x+5)*(2*x +6).

2) Пресметајте ја вредноста на функцијата во дадена точка y"(1)=8*e^0=8

Видео на темата

Корисен совет

Научете ја табелата со елементарни деривати. Ова значително ќе заштеди време.

Извори:

• дериват на константа

Значи, која е разликата помеѓу рационална равенкаод рационалното? Ако непознатата променлива е под знакот квадратен корен, тогаш равенката се смета за ирационална.

Инструкции

Главниот метод за решавање на вакви равенки е методот на конструирање на двете страни равенкиво квадрат. Сепак. ова е природно, првото нешто што треба да направите е да се ослободите од знакот. Овој метод не е технички тежок, но понекогаш може да доведе до проблеми. На пример, равенката е v(2x-5)=v(4x-7). Со квадратирање на двете страни се добива 2x-5=4x-7. Решавањето на таква равенка не е тешко; x=1. Но, бројот 1 нема да биде даден равенки. Зошто? Заменете еден во равенката наместо вредноста на x. А десната и левата страна ќе содржат изрази кои немаат смисла, т.е. Оваа вредност не важи за квадратен корен. Според тоа, 1 е надворешен корен и затоа оваа равенка нема корени.

Значи, ирационална равенка се решава со методот на квадратирање на двете негови страни. И откако ќе ја решите равенката, неопходно е да се отсечат надворешни корени. За да го направите ова, заменете ги пронајдените корени во оригиналната равенка.

Размислете за уште еден.
2х+vх-3=0
Се разбира, оваа равенка може да се реши со користење на истата равенка како претходната. Премести соединенија равенки, кои немаат квадратен корен, во десна странаа потоа користете го методот на квадратура. решете ја добиената рационална равенка и корени. Но и уште една, поелегантна. Внесете нова променлива; vх=y. Според тоа, ќе добиете равенка од формата 2y2+y-3=0. Тоа е, вообичаеното квадратна равенка. Најдете ги неговите корени; y1=1 и y2=-3/2. Следно, реши две равенки vх=1; vх=-3/2. Втората равенка нема корени, од првата откриваме дека x=1. Не заборавајте да ги проверите корените.

Решавањето на идентитетите е прилично едноставно. За да го направите ова треба да направите идентитетски трансформациидодека не се постигне целта. Така, со помош на едноставни аритметички операции, ќе се реши задачата што е на располагање.

Ќе ви треба

• - хартија;
• - пенкало.

Инструкции

Наједноставните од таквите трансформации се алгебарските скратени множење (како што е квадратот на збирот (разлика), разликата на квадратите, сумата (разликата), коцката на збирот (разликата)). Покрај тоа, постојат многу тригонометриски формули, кои во суштина се исти идентитети.

Навистина, квадратот на збирот на два члена е еднаков на квадратот на првиот плус двапати од производот на првиот за вториот и плус квадратот на вториот, односно (a+b)^2= (a+ б)(а+б)=а^2+аб +ба+б ^2=а^2+2аб+б^2.

Поедноставете ги и двете

Општи принципи на решението

Повторете од учебник по математичка анализа или виша математика што е определен интеграл. Како што е познато, решението определен интегралпостои функција чиј извод дава интегранд. Оваа функцијасе нарекува антидериват. Врз основа на овој принцип, се конструираат главните интеграли.
Одредете според типот на интеградот кој од интегралите на табелата е погоден во овој случај. Не е секогаш можно ова веднаш да се одреди. Честопати, табеларната форма станува забележлива само по неколку трансформации за да се поедностави интеграндот.

Метод за замена на променлива

Ако интеграндот е тригонометриска функција чиј аргумент е полином, тогаш обидете се да го користите методот на промена на променливите. За да го направите ова, заменете го полиномот во аргументот на интеградот со некоја нова променлива. Врз основа на односот помеѓу новите и старите променливи, утврдете ги новите граници на интеграција. Со диференцирање на овој израз, пронајдете го новиот диференцијал во . Така ќе добиете новиот видод претходниот интеграл, блиску или дури одговара на кој било табеларен.

Решавање интеграли од втор вид

Ако интегралот е интеграл од вториот вид, векторска форма на интеграндот, тогаш ќе треба да ги користите правилата за премин од овие интеграли во скаларните. Едно такво правило е релацијата Остроградски-Гаус. Овој закон ни овозможува да се движиме од роторскиот флукс на одредена векторска функција до тројниот интеграл над дивергенцијата на дадено векторско поле.

Замена на границите за интеграција

По наоѓањето на антидериватот, потребно е да се заменат границите на интеграција. Прво, заменете ја вредноста на горната граница во изразот за антидериватот. Ќе добиете некој број. Следно, од добиениот број одземете друг број добиен од долната граница во антидериватот. Ако една од границите на интеграцијата е бесконечност, тогаш кога се заменува во антидеривативна функцијапотребно е да се оди до границата и да се најде кон што се стреми изразот.
Ако интегралот е дводимензионален или тридимензионален, тогаш ќе треба геометриски да ги претставите границите на интеграцијата за да разберете како да го оцените интегралот. Навистина, во случај на, да речеме, тродимензионален интеграл, границите на интеграцијата можат да бидат цели рамнини што го ограничуваат волуменот што се интегрира.

Продолжуваме да ги проучуваме логаритмите. Во оваа статија ќе зборуваме за пресметување на логаритми, овој процес се нарекува логаритам. Прво ќе го разбереме пресметувањето на логаритмите по дефиниција. Следно, ајде да погледнеме како се наоѓаат вредностите на логаритмите користејќи ги нивните својства. После ова, ќе се фокусираме на пресметување на логаритми преку првично наведените вредности на другите логаритми. Конечно, да научиме како да користиме логаритамски табели. Целата теорија е дадена со примери со детални решенија.

Навигација на страницата.

Пресметување на логаритми по дефиниција

Во наједноставните случаи можно е да се изврши доста брзо и лесно наоѓање на логаритам по дефиниција. Ајде внимателно да погледнеме како се случува овој процес.

Неговата суштина е да го претстави бројот b во форма a c, од кој, според дефиницијата за логаритам, бројот c е вредноста на логаритамот. Односно, по дефиниција, следниот синџир на еднаквости одговара на наоѓање на логаритамот: log a b=log a a c =c.

Значи, пресметувањето на логаритам по дефиниција се сведува на наоѓање број c таков што a c = b, а самиот број c е саканата вредност на логаритамот.

Земајќи ги предвид информациите од претходните параграфи, кога бројот под знакот на логаритам е даден со одредена моќност на логаритамската основа, можете веднаш да покажете на што е еднаков логаритамот - тој е еднаков на експонентот. Ајде да покажеме решенија за примери.

Пример.

Најдете го логот 2 2 −3, а исто така пресметајте го природниот логаритам на бројот e 5,3.

Решение.

Дефиницијата на логаритамот ни овозможува веднаш да кажеме дека log 2 2 −3 =−3. Навистина, бројот под знакот на логаритам е еднаков на основата 2 до моќноста -3.

Слично, го наоѓаме вториот логаритам: lne 5.3 =5.3.

Одговор:

log 2 2 −3 =−3 и lne 5,3 =5,3.

Ако бројот b под знакот логаритам не е наведен како моќност на основата на логаритамот, тогаш треба внимателно да погледнете дали е можно да се дојде до претстава за бројот b во форма a c. Често ова претставување е сосема очигледно, особено кога бројот под знакот на логаритам е еднаков на основата со моќност од 1, или 2, или 3, ...

Пример.

Пресметај ги логаритмите log 5 25 и .

Решение.

Лесно е да се види дека 25=5 2, ова ви овозможува да го пресметате првиот логаритам: log 5 25=log 5 5 2 =2.

Ајде да продолжиме со пресметување на вториот логаритам. Бројот може да се претстави како моќност од 7: (видете ако е потребно). Оттука, .

Да го преработиме третиот логаритам во следната форма. Сега можете да го видите тоа , од што заклучуваме дека . Според тоа, по дефиниција за логаритам .

Накратко, решението би можело да се напише вака: .

Одговор:

дневник 5 25=2 , И .

Кога има доволно голем природен број под знакот на логаритам, не е повредено да се факторинг во прости фактори. Често помага да се претстави таков број како некоја моќност на основата на логаритмот, и затоа се пресметува овој логаритам по дефиниција.

Пример.

Најдете ја вредноста на логаритамот.

Решение.

Некои својства на логаритмите ви овозможуваат веднаш да ја одредите вредноста на логаритмите. Овие својства го вклучуваат својството на логаритамот на еден и својството на логаритамот на број еднаков на основата: log 1 1=log a a 0 =0 и log a a=log a 1 =1. Односно, кога под знакот на логаритмот има број 1 или број a еднаков на основата на логаритмот, тогаш во овие случаи логаритмите се еднакви на 0 и 1, соодветно.

Пример.

На што се еднакви логаритмите и log10?

Решение.

Бидејќи , тогаш од дефиницијата за логаритам следува .

Во вториот пример, бројот 10 под знакот логаритам се совпаѓа со неговата основа, така што декадниот логаритам од десет е еднаков на еден, односно lg10=lg10 1 =1.

Одговор:

И lg10=1.

Забележете дека пресметувањето на логаритмите по дефиниција (за кое разговаравме во претходниот пасус) подразбира употреба на логот за еднаквост a a p =p, што е едно од својствата на логаритмите.

Во пракса, кога број под знакот логаритам и основата на логаритамот лесно се претставени како моќност на одреден број, многу е погодно да се користи формулата , што одговара на едно од својствата на логаритмите. Ајде да погледнеме пример за наоѓање логаритам кој ја илустрира употребата на оваа формула.

Пример.

Пресметајте го логаритамот.

Решение.

Одговор:

.

Својствата на логаритмите кои не се споменати погоре се користат и во пресметките, но за ова ќе зборуваме во следните параграфи.

Наоѓање логаритми преку други познати логаритми

Информациите во овој став ја продолжуваат темата за користење на својствата на логаритмите при нивното пресметување. Но, тука главната разлика е во тоа што својствата на логаритмите се користат за изразување на оригиналниот логаритам во однос на друг логаритам, чија вредност е позната. Да дадеме пример за појаснување. Да речеме дека знаеме дека log 2 3≈1.584963, тогаш можеме да го најдеме, на пример, log 2 6 со правење мала трансформација користејќи ги својствата на логаритмот: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

Во горниот пример, доволно ни беше да го искористиме својството на логаритам на производ. Меѓутоа, многу почесто е потребно да се користи поширок арсенал на својства на логаритмите за да се пресмета оригиналниот логаритам преку дадените.

Пример.

Пресметајте го логаритамот од 27 до основата 60 ако знаете дека log 60 2=a и log 60 5=b.

Решение.

Значи треба да го најдеме дневникот 60 27 . Лесно е да се види дека 27 = 3 3 , а оригиналниот логаритам, поради својството на логаритамот на моќноста, може да се препише како 3·log 60 3 .

Сега да видиме како да го изразиме логот 60 3 во однос на познатите логаритми. Својството на логаритам на број еднаков на основата ни овозможува да го напишеме логот за еднаквост 60 60=1. Од друга страна, log 60 60=log60(2 2 3 5)= лог 60 2 2 + дневник 60 3 + лог 60 5= 2·лог 60 2+лог 60 3+лог 60 5 . Така, 2 лог 60 2+лог 60 3+лог 60 5=1. Оттука, log 60 3=1−2·log 60 2−log 60 5=1−2·a−b.

Конечно, го пресметуваме оригиналниот логаритам: log 60 27=3 log 60 3= 3·(1−2·a−b)=3−6·a−3·b.

Одговор:

log 60 27=3·(1−2·a−b)=3−6·a−3·b.

Одделно, вреди да се спомене значењето на формулата за премин кон нова основа на логаритмот на формата . Ви овозможува да се движите од логаритми со која било основа до логаритми со одредена основа, чии вредности се познати или е можно да се најдат. Обично, од оригиналниот логаритам, користејќи ја формулата за транзиција, тие се префрлаат на логаритми во една од базите 2, e или 10, бидејќи за овие бази постојат табели на логаритми кои овозможуваат нивните вредности да се пресметаат со одреден степен на точност. Во следниот пасус ќе покажеме како се прави ова.

Логаритмски табели и нивна употреба

За приближна пресметка на логаритамските вредности може да се користат логаритамски табели. Најчесто користена табела со логаритам со основа 2, табела со природен логаритам и децимална логаритамска табела. Кога работите во децимален броен систем, погодно е да се користи табела со логаритми заснована на основата десет. Со негова помош ќе научиме да ги наоѓаме вредностите на логаритмите.

Презентираната табела ви овозможува да ги пронајдете вредностите на децималните логаритми на броеви од 1.000 до 9.999 (со три децимални места) со точност од десет илјадити дел. Ќе го анализираме принципот на пронаоѓање на вредноста на логаритам користејќи табела со децимални логаритми користејќи конкретен пример - вака е појасно. Ајде да го најдеме log1.256.

Во левата колона од табелата со децимални логаритми ги наоѓаме првите две цифри од бројот 1,256, односно наоѓаме 1,2 (овој број е заокружен со сино за јасност). Третата цифра од бројот 1.256 (цифра 5) се наоѓа во првата или последната линија лево од двојната линија (овој број е заокружен со црвено). Четвртата цифра од оригиналниот број 1.256 (цифра 6) се наоѓа во првата или последната линија десно од двојната линија (овој број е заокружен со зелена линија). Сега ги наоѓаме броевите во ќелиите на табелата со логаритам на пресекот на означениот ред и означените колони (овие бројки се означени со портокалова боја). Збирот на означените броеви ја дава саканата вредност на декадниот логаритам точна до четвртото децимално место, т.е. log1.236≈0.0969+0.0021=0.0990.

Дали е можно, користејќи ја горната табела, да се најдат вредностите на децималните логаритми на броеви кои имаат повеќе од три цифри по децималната точка, како и оние што го надминуваат опсегот од 1 до 9,999? Да ти можеш. Ајде да покажеме како се прави ова со пример.

Ајде да пресметаме lg102.76332. Прво треба да запишете број во стандардна форма: 102,76332=1,0276332·10 2. По ова, мантисата треба да се заокружи на третото децимално место, имаме 1,0276332 10 2 ≈1,028 10 2, додека оригиналниот децимален логаритам е приближно еднаков на логаритамот на добиениот број, односно земаме log102.76332≈lg1.028·10 2. Сега ги применуваме својствата на логаритмот: lg1,028·10 2 =lg1,028+lg10 2 =lg1,028+2. Конечно, ја наоѓаме вредноста на логаритмот lg1.028 од табелата со децимални логаритми lg1.028≈0.0086+0.0034=0.012. Како резултат на тоа, целиот процес на пресметување на логаритам изгледа вака: log102.76332=log1.0276332 10 2 ≈lg1.028 10 2 = log1.028+lg10 2 =log1.028+2≈0.012+2=2.012.

Како заклучок, вреди да се напомене дека користејќи табела со децимални логаритми можете да ја пресметате приближната вредност на кој било логаритам. За да го направите ова, доволно е да ја користите формулата за транзиција за да отидете до децимални логаритми, да ги пронајдете нивните вредности во табелата и да ги извршите преостанатите пресметки.

На пример, да го пресметаме дневникот 2 3 . Според формулата за премин кон нова основа на логаритамот, имаме . Од табелата со децимални логаритми наоѓаме log3≈0.4771 и log2≈0.3010. Така, .

Библиографија.

• Колмогоров А.Н., Абрамов А.М., Дудницин Ју.П. и други.Алгебра и почетоците на анализа: Учебник за 10 - 11 одделение на општообразовните установи.
• Гушев В.А., Мордкович А.Г. Математика (прирачник за оние кои влегуваат во техничките училишта).

Концептот на логаритам и основниот логаритамски идентитет

Концептот на логаритам и основниот логаритамски идентитет се тесно поврзани, бидејќи дефиниција на логаритам во математичка нотацијаи е .

Основниот логаритамски идентитет произлегува од дефиницијата на логаритамот:

Дефиниција 1

Логаритамтие го нарекуваат експонентот $n$, кога ќе се подигне до кој броевите $a$ го добиваат бројот $b$.

Забелешка 1

Експоненцијална равенка$a^n=b$ за $a > 0$, $a \ne 1$ нема решенија за непозитивни $b$ и има единствен корен за позитивен $b$. Овој корен се нарекува логаритам на бројот $b$ до основата $a$и запишете:

$a^(\log_(a) b)=b$.

Дефиниција 2

Изразување

$a^(\log_(a) b)=b$

повикани основен логаритамски идентитетпод услов $a,b > 0$, $a \ne 1$.

Пример 1

$17^(\log_(17) 6)=6$;

$e^(\ln⁡13) =13$;

$10^(\lg23)=23$.

Основен логаритамски идентитет

Главналогаритамскиот идентитет се нарекува затоа што се користи скоро секогаш при работа со логаритми. Дополнително, со негова помош се поткрепени основните својства на логаритмите.

Пример 2

$7^5=16.807$, значи $\log_(7)16.807=5$.

$3^(-5)=\frac(1)(243)$, затоа $\log_(3)\frac(1)(243)=-5$.

$11^0=1$, затоа $\log_(11)⁡1=0$.

Ајде да размислиме последица на основниот логаритамски идентитет:

Дефиниција 3

Ако два логаритами со исти основи се еднакви, тогаш логаритамските изрази се еднакви:

ако $\log_(a)⁡b=\log_(a)⁡c$, тогаш $b=c$.

Ајде да размислиме ограничувања, кои се користат за логаритамскиот идентитет:

Бидејќи кога го подигаме единството на која било моќ, секогаш добиваме една, а еднаквоста $x=\log_(a)⁡b$ постои само за $b=1$, тогаш $\log_(1)⁡1$ ќе биде која било реален број. За да ја избегнете оваа нејаснотија, земете $a \ne 1$.

Логаритмот за $a=0$, според дефиницијата, може да постои само за $b=0$. Бидејќи Кога ќе подигнеме нула на која било моќност, секогаш добиваме нула, тогаш $\log_(0)⁡0$ може да биде кој било реален број. За да ја избегнете оваа нејаснотија, земете $a \ne 0$. За $а рационално и ирационаленлогаритамски вредности, бидејќи степен со рационален и ирационален експонент може да се пресмета само за позитивни основи. За да ја спречите оваа ситуација, земете $a > 0$.

$b > 0$ следи од условот $a > 0$, бидејќи $x=\log_(a)⁡b$, а моќта на позитивен број a секогаш ќе биде позитивна.

Основниот логаритамски идентитет често се користи за поедноставување на логаритамските изрази.

Пример 3

Пресметајте $81^(\log_(9) 7)$.

Решение.

За да се користи основниот логаритамски идентитет, потребно е основата на логаритамот и моќите да бидат исти. Да ја напишеме основата на степенот во форма:

Сега можеме да напишеме:

$81^(\log_(9)7)=(9^2)^(\log_(9)7)=$

Ајде да го искористиме својството моќ:

$=9^(2 \cdot \log_(9)7)=9^(\log_(9)7) \cdot 9^(\log_(9)7)=$

основниот логаритамски идентитет сега може да се примени за секој фактор:

$=7 \cdot 7=49$.

Забелешка 2

За да го примените основниот логаритамски идентитет, можете исто така да прибегнете кон замена на основата на логаритамот со изразот што се појавува под знакот логаритам, и обратно.

Пример 4

Пресметајте $7^(\frac(1)(\log_(11) 7))$.

Решение.

$7^(\frac(1)(\log_(11) 7))=7^(\log_(7) 11)=11$.

Одговори: $11$.

Пример 5

Пресметајте $7^(\frac(3)(\log_(11) 7))$.